题目内容
椭圆中心是原点O,它的短轴长为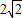 ,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l:
,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l: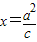 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.(Ⅰ)求椭圆的方程和离心率;
(Ⅱ)若
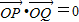 ,求直线PQ的方程;
,求直线PQ的方程;(Ⅲ)设
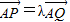 (λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明:
(λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明: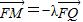 .
.
【答案】分析:(Ⅰ)首先由条件|OF|=2|FA|列式,求出椭圆的离心率,然后结合短轴长2b=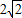 及a2=b2+c2可求a2,则椭圆方程可求;
及a2=b2+c2可求a2,则椭圆方程可求;
(Ⅱ)写出过点A的直线方程,设出直线与椭圆相交于P、Q两点的坐标,联立直线方程和椭圆方程后求出P、Q两点的横坐标的和与积,由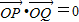 ,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;
,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;
(Ⅲ)由向量的坐标表示写出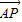 ,
,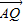 ,再由
,再由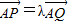 (λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.
(λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.
解答: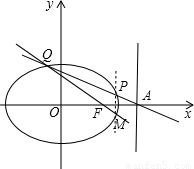 解:如图,
解:如图,
(Ⅰ)设椭圆方程为 .
.
由|OF|=2|FA|,得c=2(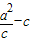 ),整理得:3c2=2a2,∴e=
),整理得:3c2=2a2,∴e=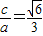 .
.
联立 ,解得:a2=6,b2=2.
,解得:a2=6,b2=2.
∴椭圆的方程为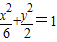 ,离心率
,离心率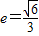 .
.
(Ⅱ)由题意可知直线l的斜率显然存在,设其斜率为k(k≠0),且A(3,0).
则直线l的方程为y=k(x-3),设P(x1,y1),Q(x2,y2).
联立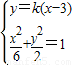 ,得:(1+3k2)x2-18k2x+27k2-6=0.
,得:(1+3k2)x2-18k2x+27k2-6=0.
由△=(-18k2)2-4(1+3k2)(27k2-6)=12(2-3k2)>0,得: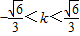 .
.
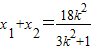 ,
,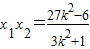 .
.
由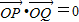 ,得x1x2+y1y2=0.
,得x1x2+y1y2=0.
即x1x2+(kx1-3k)(kx2-3k)=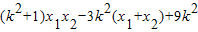
=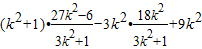 =0.
=0.
化简得: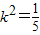 ,∴k=
,∴k= ,满足
,满足 .
.
(Ⅲ)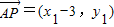 ,
,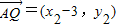 ,
,
由已知得方程组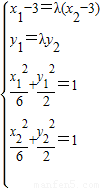 ,解得:
,解得: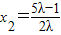 .
.
∵F(2,0),M(x1,-y1).
故 =(λ(x2-3)+1,-y1)
=(λ(x2-3)+1,-y1)
=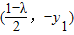 =
=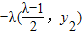 .
.
而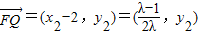 .
.
∴ .
.
点评:本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的位置关系,考查了数形结合的解题思想,解答此类问题的关键是,常常采用设而不求的方法,即设出直线与圆锥曲线交点的坐标,解答时不求坐标,而是运用根与系数关系求出两个点的横坐标的和与积,然后结合已知条件整体代入求解问题,此题还应注意的是要保证直线和椭圆交点的存在性,此题是难题.
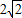 及a2=b2+c2可求a2,则椭圆方程可求;
及a2=b2+c2可求a2,则椭圆方程可求;(Ⅱ)写出过点A的直线方程,设出直线与椭圆相交于P、Q两点的坐标,联立直线方程和椭圆方程后求出P、Q两点的横坐标的和与积,由
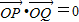 ,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;
,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;(Ⅲ)由向量的坐标表示写出
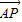 ,
,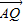 ,再由
,再由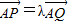 (λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.
(λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.解答:
 解:如图,
解:如图,(Ⅰ)设椭圆方程为
 .
.由|OF|=2|FA|,得c=2(
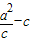 ),整理得:3c2=2a2,∴e=
),整理得:3c2=2a2,∴e=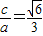 .
.联立
 ,解得:a2=6,b2=2.
,解得:a2=6,b2=2.∴椭圆的方程为
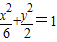 ,离心率
,离心率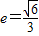 .
.(Ⅱ)由题意可知直线l的斜率显然存在,设其斜率为k(k≠0),且A(3,0).
则直线l的方程为y=k(x-3),设P(x1,y1),Q(x2,y2).
联立
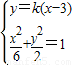 ,得:(1+3k2)x2-18k2x+27k2-6=0.
,得:(1+3k2)x2-18k2x+27k2-6=0.由△=(-18k2)2-4(1+3k2)(27k2-6)=12(2-3k2)>0,得:
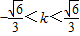 .
.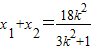 ,
,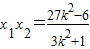 .
.由
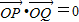 ,得x1x2+y1y2=0.
,得x1x2+y1y2=0.即x1x2+(kx1-3k)(kx2-3k)=
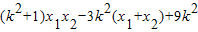
=
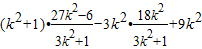 =0.
=0.化简得:
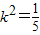 ,∴k=
,∴k= ,满足
,满足 .
.(Ⅲ)
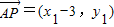 ,
,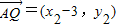 ,
,由已知得方程组
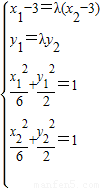 ,解得:
,解得: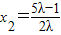 .
.∵F(2,0),M(x1,-y1).
故
 =(λ(x2-3)+1,-y1)
=(λ(x2-3)+1,-y1)=
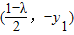 =
=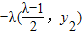 .
.而
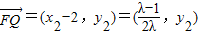 .
.∴
 .
.点评:本题考查了椭圆标准方程的求法,考查了直线和圆锥曲线的位置关系,考查了数形结合的解题思想,解答此类问题的关键是,常常采用设而不求的方法,即设出直线与圆锥曲线交点的坐标,解答时不求坐标,而是运用根与系数关系求出两个点的横坐标的和与积,然后结合已知条件整体代入求解问题,此题还应注意的是要保证直线和椭圆交点的存在性,此题是难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目