题目内容
已知以角B为钝角的△ABC的内角A、B、C的对边分别为a、b、c, ,且
,且 .(1)求角B的大小;(2)求cosA+cosC的取值范围.
.(1)求角B的大小;(2)求cosA+cosC的取值范围.
解:(1)∵ .∴
.∴ ,得
,得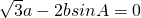 (2分)
(2分)
由正弦定理,得a=2RsinA,b=2RsinB,代入得:(3分)
 sinA-2sinBsinA=0,sinA≠0,
sinA-2sinBsinA=0,sinA≠0,
∴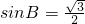 ,(5分)
,(5分)
B为钝角,所以角 .(7分)
.(7分)
(2)(理科)∵cosA+cosC=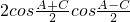 =
=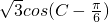
(或:cosA+cosC=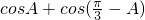 =
=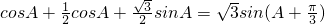 )(10分)
)(10分)
由(1)知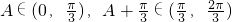 ,
,
∴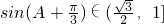 (12分)
(12分)
故cosA+cosC的取值范围是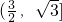
分析:(1)利用 ,结合正弦定理,求出
,结合正弦定理,求出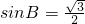 ,B为钝角,所以角
,B为钝角,所以角 .
.
(2)利用和差化积化简cosA+cosC=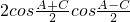 =
=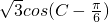 ,由(1)知
,由(1)知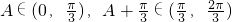 ,确定cosA+cosC的取值范围即可.
,确定cosA+cosC的取值范围即可.
点评:本题是基础题,考查三角函数的化简与求值,余弦定理的应用,平面向量的数量积的应用,考查计算能力,常考题型.
 .∴
.∴ ,得
,得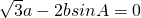 (2分)
(2分)由正弦定理,得a=2RsinA,b=2RsinB,代入得:(3分)
 sinA-2sinBsinA=0,sinA≠0,
sinA-2sinBsinA=0,sinA≠0,∴
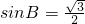 ,(5分)
,(5分)B为钝角,所以角
 .(7分)
.(7分)(2)(理科)∵cosA+cosC=
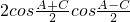 =
=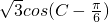
(或:cosA+cosC=
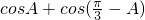 =
=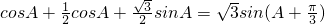 )(10分)
)(10分)由(1)知
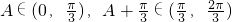 ,
,∴
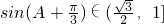 (12分)
(12分)故cosA+cosC的取值范围是
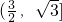
分析:(1)利用
 ,结合正弦定理,求出
,结合正弦定理,求出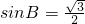 ,B为钝角,所以角
,B为钝角,所以角 .
.(2)利用和差化积化简cosA+cosC=
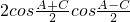 =
=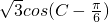 ,由(1)知
,由(1)知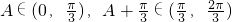 ,确定cosA+cosC的取值范围即可.
,确定cosA+cosC的取值范围即可.点评:本题是基础题,考查三角函数的化简与求值,余弦定理的应用,平面向量的数量积的应用,考查计算能力,常考题型.

练习册系列答案
相关题目
 ,
, ,且
,且 .
. 的取值范围.
的取值范围.