题目内容
F1、F2为椭圆 的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|等于
的两个焦点,过F1的直线交椭圆于A、B两点,若|F2A|+|F2B|=12,则|AB|等于
- A.6
- B.8
- C.5
- D.4
B
分析:由椭圆的定义得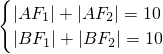 ,所以|AB|+|AF2|+|BF2|=20,由此可求出|AB|的长.
,所以|AB|+|AF2|+|BF2|=20,由此可求出|AB|的长.
解答:由椭圆的定义得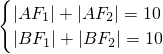
两式相加得|AB|+|AF2|+|BF2|=20,
即|AB|+12=20,
∴|AB|=8.
故选B
点评:本题考查椭圆的基本性质和应用,解题时要注意公式的合理运用.
分析:由椭圆的定义得
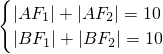 ,所以|AB|+|AF2|+|BF2|=20,由此可求出|AB|的长.
,所以|AB|+|AF2|+|BF2|=20,由此可求出|AB|的长.解答:由椭圆的定义得
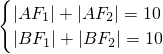
两式相加得|AB|+|AF2|+|BF2|=20,
即|AB|+12=20,
∴|AB|=8.
故选B
点评:本题考查椭圆的基本性质和应用,解题时要注意公式的合理运用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目