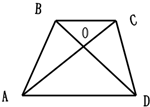
题目内容
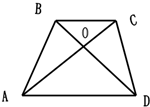如图，| AB |
| BC |
| CD |
| BC |
| AD |
（1）求x与y间的关系；
（2）若
| AC |
| BD |
分析：（1）根据向量的加法法则得到
=
+
+
=（4+x，y-2），再根据向量共线的充要条件，即可得出x与y间的关系；
（2）先表示出
=
+
=（6+x，1+y），
=（x-2，y-3）．再根据向量垂直的充要条件，即可得出
和
的坐标，从而求得四边形ABCD的面积．
| AD |
| AB |
| BC |
| CD |
（2）先表示出
| AC |
| AB |
| BC |
| BD |
| BC |
| AD |
解答：解：（1）∵
=
+
+
=（4+x，y-2），
∴由
∥
，得x（y-2）=y（4+x），
故x+2y=0．
（2）由
=
+
=（6+x，1+y），
=（x-2，y-3）．
∵
⊥
，∴（6+x）（x-2）+（1+y）（y-3）=0，又x+2y=0，
∴
或
∴当
=（-6，3）时，
=（-2，1），
当
=（2，-1）时，
=（6，-3）．
故
与
同向，
四边形ABCD的面积=
×|
|×|
|=16
| AD |
| AB |
| BC |
| CD |
∴由
| BC |
| AD |
故x+2y=0．
（2）由
| AC |
| AB |
| BC |
| BD |
∵
| AC |
| BD |
∴
|
|
∴当
| BC |
| AD |
当
| BC |
| AD |
故
| BC |
| AD |
四边形ABCD的面积=
| 1 |
| 2 |
| AC |
| DB |
点评：本题主要考查了平面向量共线（平行）的坐标表示，数量积判断两个平面向量的垂直关系．考查数形结合思想，属于中档题．
练习册系列答案
步步高达标卷系列答案
相关题目
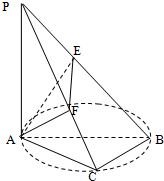如图，AB是圆O的直径，C是圆O上的点，PA垂直于圆O所在平面，AE⊥PB于E，AF⊥PC于F
已知函数f（x）=2cos2
已知如图，AB为⊙O的直径，PA、PC是⊙O的切线，A、C为切点，∠BAC=30°．