题目内容
已知函数![]() 在区间
在区间![]() 内各有一个极值点.
内各有一个极值点.
(Ⅰ)求![]() 的最大值;
的最大值;
(Ⅱ)当![]() 时,设函数
时,设函数![]() 在点
在点![]() 处的切线为
处的切线为![]() ,若
,若![]() 在点A处穿过
在点A处穿过![]() 的图象(即动点在点A附近沿曲线
的图象(即动点在点A附近沿曲线![]() 运动,经过点A时,从
运动,经过点A时,从![]() 的一侧进入另一侧),求函数
的一侧进入另一侧),求函数![]() 的表达式.
的表达式.
解:(I)因为函数![]() 在区间
在区间![]() ,
,![]() 内分别有一个极值点,所以
内分别有一个极值点,所以![]()
![]() 在
在![]() ,
,![]() 内分别有一个实根,
内分别有一个实根,
设两实根为![]() (
(![]() ),则
),则![]() ,且
,且![]() .于是
.于是
![]() ,
,![]() ,且当
,且当![]()
![]() ,即
,即![]() ,
,![]() 时等号成立.故
时等号成立.故![]() 的最大值是16.
的最大值是16.
(Ⅱ)解法一:由![]() 知
知![]() 在点
在点![]() 处的切线
处的切线![]() 的方程是
的方程是
![]() ,即
,即![]() ,
,
因为切线![]() 在点
在点![]() 处穿过
处穿过![]() 的图象,
的图象,
所以![]() 在
在![]() 两边附近的函数值异号,则
两边附近的函数值异号,则
![]() 不是
不是![]() 的极值点.
的极值点.
而![]()
![]() ,且
,且
![]() .
.
若![]() ,则
,则![]() 和
和![]() 都是
都是![]() 的极值点.
的极值点.
所以![]() ,即
,即![]() ,又由
,又由![]() ,得
,得![]() ,故
,故![]() .
.
解法二:同解法一得![]()
![]() .
.
因为切线![]() 在点
在点![]() 处穿过
处穿过![]() 的图象,所以
的图象,所以![]() 在
在![]() 两边附近的函数值异号,于是存在
两边附近的函数值异号,于是存在![]() (
(![]() ).
).
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
或当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
设![]() ,则
,则
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ;
;
或当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
由![]() 知
知![]() 是
是![]() 的一个极值点,则
的一个极值点,则![]() ,
,
所以![]() ,又由
,又由![]() ,得
,得![]() ,故
,故![]() .
.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 ,在区间
,在区间 内各有一个极值点。直线
内各有一个极值点。直线 是函数
是函数 在点
在点 处的切线。
处的切线。 的取值范围。
的取值范围。 处穿过函数
处穿过函数 的图像,求实数
的图像,求实数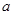 的值。
的值。 在区间
在区间 ,
, 内各有一个极值点.
内各有一个极值点. 的最大值;
的最大值; 时,设函数
时,设函数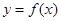 在点
在点 处的切线为
处的切线为 ,若
,若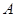 处穿过函数
处穿过函数 的表达式.
的表达式.