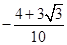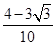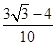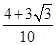题目内容
已知函数 ,其图象相邻的两条对称轴方程为
,其图象相邻的两条对称轴方程为 与
与 ,则( )
,则( )
A. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为单调递增函数 上为单调递增函数 |
B. 的最小正周期为 的最小正周期为 ,且在 ,且在 上为单调递减函数 上为单调递减函数 |
C. 的最小正周期为 的最小正周期为 ,且在 ,且在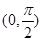 上为单调递增函数 上为单调递增函数 |
D. 的最小正周期为 的最小正周期为 ,且在 ,且在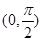 上为单调递减函数 上为单调递减函数 |
C.
解析试题分析:函数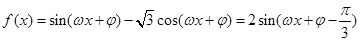 ,因相邻的两条对称轴方程为
,因相邻的两条对称轴方程为 与
与 ,所以函数的最小正周期为
,所以函数的最小正周期为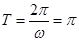 ,即
,即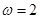 ,则原函数
,则原函数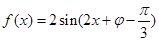 ,那么
,那么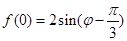 ,
, ,则
,则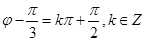 ,又因
,又因 ,得
,得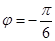 ,所以
,所以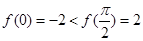 ,即函数
,即函数 在
在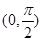 上为单调增函数.
上为单调增函数.
考点:三角函数的运算和性质.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
已知 ,则函数
,则函数 的最大值是( )
的最大值是( )
| A.3 | B. | C. | D. |
若 且
且 ,则
,则 ( )
( )
A. | B. | C.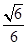 | D. |
已知 ,函数
,函数 在
在 上单调递增,则
上单调递增,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知函数f(x)=sin(ωx+ )(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
)(x∈R,ω>0)的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象( )
A.向左平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向右平移 个单位长度 个单位长度 |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
为了得到函数 的图象,可以将函数
的图象,可以将函数 的图象( )
的图象( )
A.向右平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向左平移 个单位长度 个单位长度 |
(5分)函数 的部分图象如图所示,则ω,φ的值分别是( )
的部分图象如图所示,则ω,φ的值分别是( )
A. | B. | C. | D. |
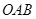 中,点
中,点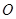 为原点,点
为原点,点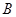 的坐标是
的坐标是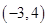 ,点
,点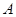 在第一象限,向量
在第一象限,向量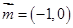 ,记向量
,记向量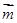 与向量
与向量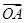 的夹角为
的夹角为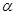 ,则
,则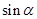 的值为( )
的值为( )