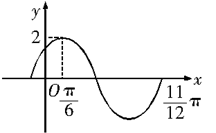
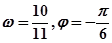题目内容
已知 ,
, ,
, ,且函数
,且函数 的最大值为
的最大值为 ,最小值为
,最小值为 。
。
(1)求 的值;
的值;
(2)(ⅰ)求函数 的单调递增区间;
的单调递增区间;
(ⅱ)求函数 的对称中心.
的对称中心.
 ,
, ,
, ,且函数
,且函数 的最大值为
的最大值为 ,最小值为
,最小值为 。
。(1)求
 的值;
的值;(2)(ⅰ)求函数
 的单调递增区间;
的单调递增区间;(ⅱ)求函数
 的对称中心.
的对称中心.(1)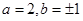 (2)(i)
(2)(i)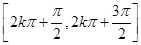 (ii)
(ii) 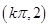 .
.
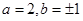 (2)(i)
(2)(i)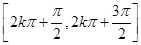 (ii)
(ii) 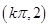 .
.试题分析:(1)根据
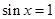 时,函数取得最大值,当
时,函数取得最大值,当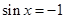 时,函数取得最小值,代入即可求得
时,函数取得最小值,代入即可求得 的值;
的值;(2)(i)
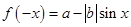 ,函数的单调性与
,函数的单调性与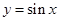 的单调性相反,
的单调性相反,(ii函数的对称中心,当
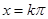 时,算出
时,算出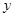 ,即求得对称中心.
,即求得对称中心.(1)由条件得
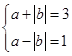 ,解得
,解得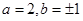 (4分)
(4分)(2)有上知:

(ⅰ)
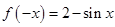 ,函数的单调性与
,函数的单调性与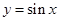 的单调性相反,
的单调性相反,所以函数
 的单调递增区间为
的单调递增区间为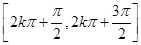 ,
,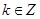 (3分)
(3分)(ⅱ)当
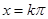 时,
时,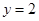 ,所以函数
,所以函数 的对称中心为
的对称中心为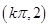 . (3分)
. (3分)
练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 、
、 的夹角为
的夹角为 (即
(即 ),现有可供建造第三面围墙的材料
),现有可供建造第三面围墙的材料 米(两面墙的长均大于
米(两面墙的长均大于 ,问当
,问当 为多少时,所建造的三角形露天仓库的面积最大,并求出最大值?
为多少时,所建造的三角形露天仓库的面积最大,并求出最大值? 
 在函数
在函数 的图象上移动,动点
的图象上移动,动点 满足
满足 ,则动点
,则动点 的轨迹方程为( )
的轨迹方程为( )



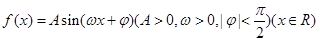 的部分图象如图所示.
的部分图象如图所示.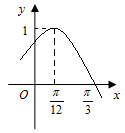
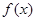 的表达式;
的表达式;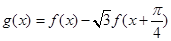 ,求函数
,求函数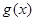 的最小值及相应的
的最小值及相应的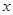 的取值集合.
的取值集合.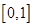 上单调递增的是
上单调递增的是


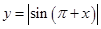
 (ω>0)的图像向左平移
(ω>0)的图像向左平移 个单位,得到函数y=g(x)的图象.
个单位,得到函数y=g(x)的图象. 上为增函数,则ω的最大值为________.
上为增函数,则ω的最大值为________.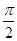 )内递增的是( )
)内递增的是( )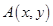 在圆
在圆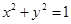 上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间
上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间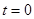 时,
时,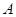 坐标是
坐标是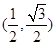 ,则当
,则当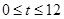 时,动点
时,动点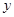 关于
关于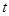 (秒)的函数的单调递增区间是( )
(秒)的函数的单调递增区间是( )


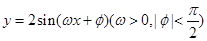 的图象上的一段,则( )
的图象上的一段,则( )