题目内容
调查在2~3级风时的海上航行中男女乘客的晕船情况,共调查了71人,其中女性34人,男性37人。女性中有10人晕船,另外24人不晕船;男性中有12人晕船,另外25人不晕船。
判断晕船是否与性别有关系。
解:假设“晕船与性别无关”,
2×2的列联表:
计算 晕船情况
性别晕船 不晕船 总计 女 10 24 34 男 12 25 37 总计 22 49 71 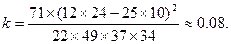
因为k<2.706,所以我们没有理由说“晕船与性别有关”。
解析

下表是关于某设备的使用年限(年)和所需要的维修费用y (万元)的几组统计数据:
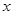 | 2 | 3 | 4 | 5 | 6 |
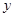 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
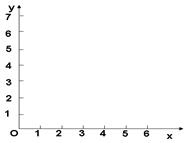
(2)请根据散点图,判断y与x之间是否有较强线性相关性,若有求线性回归直线方程
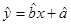 ;
;(3)估计使用年限为10年时,维修费用为多少?
(参考数值:
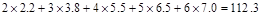 )
)参考公式:
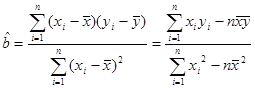 ;
;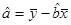 ;
; (本小题满分12分)品厂为了检查甲、乙两条自动包装流水线的生产情况,在这两条
流水线上各抽取40件产品作为样本称 出它们的重量(单位:克),重量值落在(495,510]
出它们的重量(单位:克),重量值落在(495,510]
的产 品为合格品,否则为不合格品,表1是甲流水线样本频数分布表,
品为合格品,否则为不合格品,表1是甲流水线样本频数分布表, 图1是乙流水线样
图1是乙流水线样
本的频率分布直方图。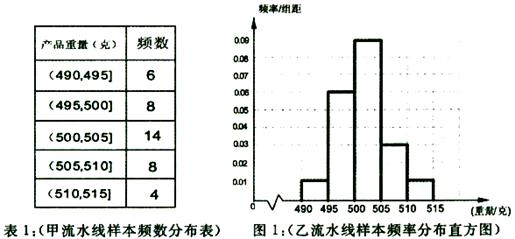 某食
某食
(1)若检验员不小心将甲、乙两条流水线生产的重量值在(510,515]的产品放在了一起,
然后又随机取出3件产品,求至少有一件是乙流水线生产的产品的概率;
(2)由以上统计数据完成下面2×2列联表,并回答有多大的把握认为“产品的包装质量
与两条自动包装流水线的选择有关”。
| | 甲流水线 | 乙流水线 | 合 计 |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | | | n= |
(本小题满分为12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了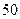 名学生。调査结果表明:在爱看课外书的
名学生。调査结果表明:在爱看课外书的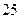 人中有
人中有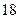 人作文水平好,另
人作文水平好,另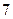 人作文水平一般;在不爱看课外书的
人作文水平一般;在不爱看课外书的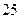 人中有
人中有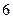 人作文水平好,另
人作文水平好,另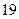 人作文水平一般.
人作文水平一般.
(Ⅰ)试根据以上数据建立一个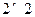 列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文
列联表,并运用独立性检验思想,指出有多大把握认为中学生的作文 水平与爱看课外书有关系?
水平与爱看课外书有关系?
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为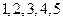 ,某
,某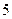 名爱看
名爱看 课外书且作文水平一般的学生也分别编号为
课外书且作文水平一般的学生也分别编号为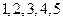 ,从这两组学生中各任选
,从这两组学生中各任选 人进行学习交流,求被选取的两名学生的编号之和为
人进行学习交流,求被选取的两名学生的编号之和为 的倍数或
的倍数或 的倍数的概率.
的倍数的概率.
附: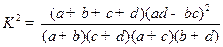
临界值表:
 | 0. 10 | 0. 05 | 0. 025 | 0.010 | 0. 005 | 0. 001 |
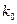 | 2. 706 | 3. 841 | 5. 024 | 6. 635 | 7. 879 | 10. 828 |
 学共有学生2000名,各年级男、女生人数如下表:
学共有学生2000名,各年级男、女生人数如下表:


 ,
, ,求高三年级
,求高三年级 中女生比男生多的概率.
中女生比男生多的概率. 意
意 量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多.
量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有9人认为作业多,3人认为作业不多;在不喜欢玩电脑游戏的10人中,有4人认为作业多,6人认为作业不多. 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系? ,
, ,可能用到数据:
,可能用到数据: ,
, ,
, ,
, .)
.)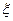 ,求
,求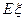 .
.