题目内容
设函数f(x)=ax2+bx+c(a>0),且f(1)=-![]() .
.
(Ⅰ)求证函数f(x)有两个零点;
(Ⅱ)设x1,x2是函数f(x)的两个零点,求|x1-x2|的范围;
(Ⅲ)求证函数f(x)的零点x1,x2至少有一个在区间(0,2)内.
答案:
解析:
解析:
|
(Ⅰ)证明: (Ⅱ)若 (Ⅲ) 由(I)知 (ⅰ)当 又 (ⅱ)当 综合(ⅰ)(ⅱ),可知函数 |

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
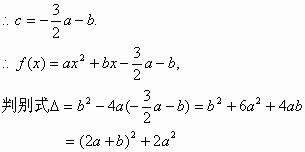
 (a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方
(a,b∈Z),曲线y=f(x)在点(2,f(2))处的切线方