题目内容
某人从2010年起,每年1月1日到银行新存入a元(一年定期),若年利率为r保持不变,且每年到期存款和利息自动转为新的一年定期,到2013年底将所有存款及利息全部取回,则可取回的钱数(元)为( )
分析:由题意可得存入a元,一年后存款及利息是a(1+r),二年后存款及利息是a(1+r)2,三年后存款及利息是a(1+r)3,由等比数列的求和公式可得.
解答:解:存入a元,一年后存款及利息是a(1+r),
二年后存款及利息是a(1+r)2,
三年后存款及利息是a(1+r)3,
则到2013年年底将所有存款及利息总数是:
a(1+r)+a(1+r)2+a(1+r)3=
=
[(1+r)4-(1+r)]
故选B
二年后存款及利息是a(1+r)2,
三年后存款及利息是a(1+r)3,
则到2013年年底将所有存款及利息总数是:
a(1+r)+a(1+r)2+a(1+r)3=
| a(1+r)[1-(1+r)3] |
| 1-(1+r) |
=
| a |
| r |
故选B
点评:本题考查等比数列的求和公式,把实际问题抽象为数列问题是解决问题的关键,属中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
某人从2010年9月1日起,每年这一天到银行存款一年定期1万元,且每年到期的存款将本和利再存入新一年的一年定期,若一年定期存款利率2.50%保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为( )
| A、11314元 | B、53877元 | C、11597元 | D、63877元 |
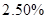 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】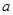 元(一年定期),若年利率为r保持不变,且每年到期存款自动转为新的一年定期,到2010年1月1日将所有存款及利息全部取回,他可取回的钱数为(单位为元) (
)
元(一年定期),若年利率为r保持不变,且每年到期存款自动转为新的一年定期,到2010年1月1日将所有存款及利息全部取回,他可取回的钱数为(单位为元) (
) 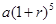 B.
B. 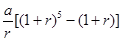 C.
C.
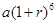 D.
D. 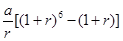
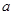 元(一年定期),若年利率为r保持不变,且
元(一年定期),若年利率为r保持不变,且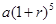 B.
B. 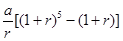 C.
C.
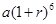 D.
D. 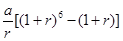 [来源:学,科,网Z,X,X,K]
[来源:学,科,网Z,X,X,K]