题目内容
某人从2010年9月1日起,每年这一天到银行存款一年定期1万元,且每年到期的存款将本和利再存入新一年的一年定期,若一年定期存款利率2.50%保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为( )
| A、11314元 | B、53877元 | C、11597元 | D、63877元 |
分析:2014年9月1日存款到2015年9月1日取回钱数记为a1,2013年9月1日存款到2015年9月1日取回钱数记为a2,依此类推,2010年9月1日存款到2015年9月1日取回钱数记为a5;a1,a2,…,a5组成等比数列{an},求它的前5项和即可.
解答:解:2014年9月1日存款到2015年9月1日取回钱数(万元)记为:a1=(1+2.5%);
2013年9月1日存款到2015年9月1日取回钱数(万元)记为:a2=(1+2.5%)2;
依此类推,2010年9月1日存款到2015年9月1日取回钱数(万元)记为:a5=(1+2.5%)5;
a1,a2,…a5组成等比数列{an},它的前5项和为:
s5=
=
=
≈5.3877(万元)=53877(元);
故应选:C.
2013年9月1日存款到2015年9月1日取回钱数(万元)记为:a2=(1+2.5%)2;
依此类推,2010年9月1日存款到2015年9月1日取回钱数(万元)记为:a5=(1+2.5%)5;
a1,a2,…a5组成等比数列{an},它的前5项和为:
s5=
| a1(1-q5) |
| 1-q |
| (1+2.5%)[1-(1+2.5%)5] |
| 1-(1+2.5%) |
| 1.025×[1-1.0255] |
| -0.025 |
故应选:C.
点评:本题考查了等比数列的概念以及前n项和的公式的应用,计算时要借助于计算器,是基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
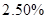 保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】
保持不变,到2015年9月1日将所有的存款和利息全部取出,他可取回的钱数约为 【 】