题目内容
如图,在椭圆C: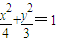 中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.
中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.(1)求证:IG∥F1F2;
(2)已知A为椭圆C的左顶点,直线l过右焦点F2与椭圆C交于M,N两点,若AM,AN的斜率k1,k2满足
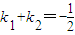 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(1)欲证IG∥F1F2,因为F1,F2在x轴上,只需证明I,G的纵坐标相等即可,利用重心的坐标公式求出G点的纵坐标,再借助三角形内切圆的性质,利用面积相等求出I的纵坐标,比较大小即可.
(2)设出直线l的方程,代入椭圆方程,由韦达定理求出x1+x2,x1x2.代入k1+k2中,化简即可求出k的值,得到直线l的方程.
解答:解:(1)设P点坐标为(x,y)(y>0),而G为△PF1F2
的重心,故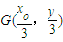 而I为△PF1F2的内心.
而I为△PF1F2的内心.
设△PF1F2的内切圆半径为r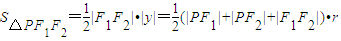
于是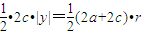 ,
,
又a=2,c=1,y>0
则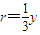 ,从而I点纵坐标为
,从而I点纵坐标为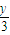
从而IG∥F1F2•
(2)若直线l斜率不存在,显然k1+k2=0不合题意.
若直线l的斜率存在,过F2(1,O)的设直线方程为y=k(x-1),直线和椭圆交于M(x1,y1),N(x2,y2)将y=k(x-1)代入3x2+4y2=12中得到:(3+4k2)x2-8k2x+4k2-12=0
由韦达定理可知: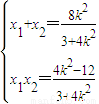
又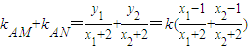 =
=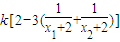
而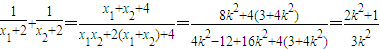
从而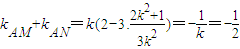
即k=2
故所求直线MN方程为:y=2(x-1).
点评:本题主要考查了直线与椭圆位置关系的判断,注意韦达定理的应用.
(2)设出直线l的方程,代入椭圆方程,由韦达定理求出x1+x2,x1x2.代入k1+k2中,化简即可求出k的值,得到直线l的方程.
解答:解:(1)设P点坐标为(x,y)(y>0),而G为△PF1F2
的重心,故
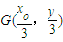 而I为△PF1F2的内心.
而I为△PF1F2的内心.设△PF1F2的内切圆半径为r
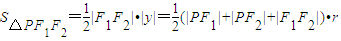
于是
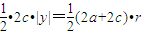 ,
,又a=2,c=1,y>0
则
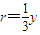 ,从而I点纵坐标为
,从而I点纵坐标为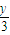
从而IG∥F1F2•
(2)若直线l斜率不存在,显然k1+k2=0不合题意.
若直线l的斜率存在,过F2(1,O)的设直线方程为y=k(x-1),直线和椭圆交于M(x1,y1),N(x2,y2)将y=k(x-1)代入3x2+4y2=12中得到:(3+4k2)x2-8k2x+4k2-12=0
由韦达定理可知:
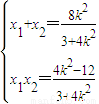
又
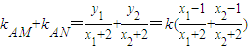 =
=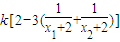
而
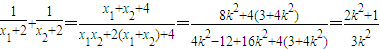
从而
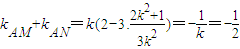
即k=2
故所求直线MN方程为:y=2(x-1).
点评:本题主要考查了直线与椭圆位置关系的判断,注意韦达定理的应用.

练习册系列答案
相关题目
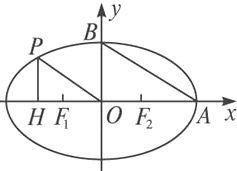 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.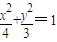 中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.
中,F1,F2分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,△PF1F2的重心为G,内心为I.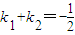 ,求直线l的方程.
,求直线l的方程.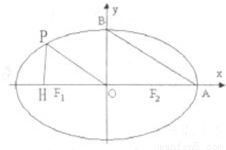 如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.
如图,在椭圆C中,点F1是左焦点,A(a,0),B(0,b)分别为右顶点和上顶点,点O为椭圆的中心.又点P在椭圆上,且满足条件:OP∥AB,点H是点P在x轴上的射影.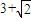 ,求椭圆的方程.
,求椭圆的方程.