题目内容
【题目】如图，在长方体
中，
，
，
，M为AB的中点，点P在线段
上，点P到直线
的距离的最小值为________.
【答案】
【解析】
连接MC，运用线面平行的判定定理可得BB'∥平面MCC'，点P到直线BB'的距离的最小值转化为异面直线BB'和直线MC'的距离，即为直线BB'和平面MCC'的距离，即为B到平面MCC'的距离，过B在底面AC内作BH⊥MC，证得BH⊥平面MCC'，求得BH的长即为所求.
解：连接MC，由BB'∥CC'，BB'平面MCC'，CC'平面MCC'，
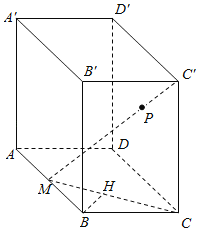
可得BB'∥平面MCC'，
由点P到直线BB'的距离的最小值为异面直线BB'和直线C'M的距离，
即有直线BB'和平面MCC'的距离即为异面直线BB'和MC'的距离，
也即B到平面MCC'的距离，
过B在底面AC内作BH⊥MC，
由CC'⊥底面AC，可得CC'⊥BH，
即有BH⊥平面MCC'，
由BC＝BM＝1，且BC⊥BA，可得BH＝.
故答案为：.
优生乐园系列答案
新编小学单元自测题系列答案【题目】为了解某校学生参加社区服务的情况，采用按性别分层抽样的方法进行调查.已知该校共有学生960人，其中男生560人，从全校学生中抽取了容量为
的样本，得到一周参加社区服务的时间的统计数据好下表：
超过1小时 | 不超过1小时 | |
男 | 20 | 8 |
女 | 12 | m |
（Ⅰ）求
，；
（Ⅱ）能否有95%的把握认为该校学生一周参加社区服务时间是否超过1小时与性别有关？
（Ⅲ）以样本中学生参加社区服务时间超过1小时的频率作为该事件发生的概率，现从该校学生中随机调查6名学生，试估计6名学生中一周参加社区服务时间超过1小时的人数.
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】（题文）从某校高一年级随机抽取
名学生，获得了他们日平均睡眠时间（单位：小时）的数据，整理得到数据分组及频数分布表：
组号 | 分组 | 频数 | 频率 |
|
|
|
|
|
|
| |
|
|
| |
|
|
| |
|
|
|
（Ⅰ）求的值．
（Ⅱ）若
，补全表中数据，并绘制频率分布直方图．
（Ⅲ）假设同一组中的每个数据可用该组区间的中点值代替，若上述数据的平均值为
，求
，
的值，并由此估计该校高一学生的日平均睡眠时间不少于
小时的概率．
