题目内容
已知 为
为 的内角,且
的内角,且 ,则
,则 .
.
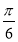 或
或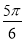
【解析】
试题分析:依题意可知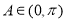 ,且
,且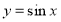 在
在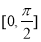 单调递增,所以当
单调递增,所以当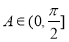 时,
时, 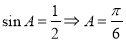 ,当
,当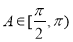 时,
时,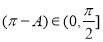 ,所以
,所以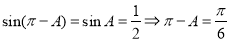 ,即
,即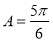 ,综上可知
,综上可知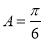 或
或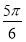 .
.
考点:1.三角形内角的取值范围;2.正弦函数的单调性.

练习册系列答案
相关题目
题目内容
已知 为
为 的内角,且
的内角,且 ,则
,则 .
.
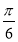 或
或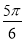
【解析】
试题分析:依题意可知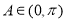 ,且
,且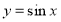 在
在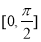 单调递增,所以当
单调递增,所以当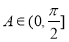 时,
时, 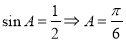 ,当
,当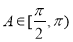 时,
时,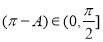 ,所以
,所以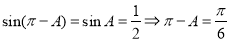 ,即
,即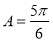 ,综上可知
,综上可知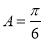 或
或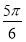 .
.
考点:1.三角形内角的取值范围;2.正弦函数的单调性.
