题目内容
在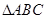 中,
中,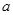 、
、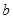 、
、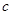 分别是角
分别是角 、
、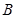 、
、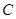 的对边,
的对边,
且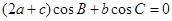 .
.
(Ⅰ)求角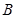 的值;
的值;
(Ⅱ)已知函数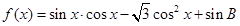 ,求
,求 的单调递增区间
的单调递增区间
【答案】
(Ⅰ)由正弦定理得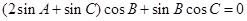 ,
,
即
得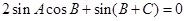 ..........3分
..........3分
因为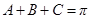 ,所以
,所以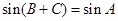 ,得
,得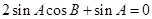 ,
,
因为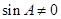 , 所以
, 所以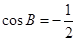 ,
,
又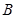 为三角形的内角,所以
为三角形的内角,所以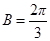 ......6分
......6分
(Ⅱ) 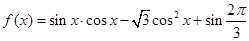
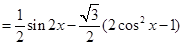
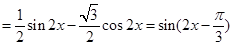
由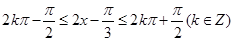 得
得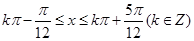
故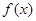 的单调递增区间为:
的单调递增区间为: 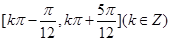
【解析】略

练习册系列答案
相关题目





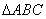
 中,
中,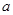 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,
的对边, ,且符合
,且符合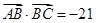 .
. ,求角
,求角 ,
, ,设函数
,设函数 .
.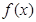 的最小正周期与单调递增区间.(2)在
的最小正周期与单调递增区间.(2)在 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若 的面积为
的面积为 ,求
,求 中,
中, 、
、 、
、 分别是角
分别是角 所对的边,
所对的边, 60º,
60º, ,△
,△ =
= ,则
,则 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,且
的对边,且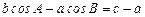 .
. ,且
,且 ,求
,求