题目内容
已知函数 的定义域为
的定义域为 ,值域为
,值域为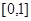 ,那么满足条件的整数对
,那么满足条件的整数对 共有 ( )
共有 ( )
 的定义域为
的定义域为 ,值域为
,值域为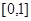 ,那么满足条件的整数对
,那么满足条件的整数对 共有 ( )
共有 ( )A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
C
分析:由题设,值域是[0,1],可得1≤
 ≤2,由此解出0≤|x|≤2,由于x=0时y=1,x=±2时,y=0,故在定义域中一定有0,而±2必有其一,当一定有2时,取b=2时,a可取-2,-1,0,当b=-2时,a可取0,1
≤2,由此解出0≤|x|≤2,由于x=0时y=1,x=±2时,y=0,故在定义域中一定有0,而±2必有其一,当一定有2时,取b=2时,a可取-2,-1,0,当b=-2时,a可取0,1解:由题意函数f(x)=
 -1的值域是[0,1],
-1的值域是[0,1],∴1≤
 ≤2
≤2∴0≤|x|≤2
∴-2≤x≤2
∴[a,b]?[-2,2]
由于x=0时y=1,x=±2时,y=0,故在定义域中一定有0,而±2必有其一,又a,b∈Z
取b=2时,a可取-2,-1,0,取a=-2时,b可取0,1
故满足条件的整数数对(a,b)共有5对
故应选C.

练习册系列答案
相关题目
 满足
满足 ,则
,则 的值是()
的值是()



 在
在 上有实根,则
上有实根,则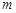 的取值范围是( )
的取值范围是( )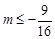



 的值域为
的值域为 ,且
,且 ,则
,则 的最大值为( )
的最大值为( )
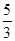


 及两点
及两点 和
和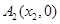 ,其中
,其中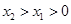 .过
.过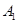 ,
, 分别作
分别作 轴的垂线,交曲线
轴的垂线,交曲线 于
于 ,
, 两点,直线
两点,直线 与
与 ,那么
,那么 成等差数列
成等差数列 成等差数列
成等差数列 那么
那么




 则函数
则函数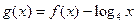 的零点个数为( )
的零点个数为( )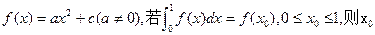 的值是 。
的值是 。