题目内容
班主任为了对本班学生的考试成绩进行分析,决定从全班25名女同学,15名男同学中随机抽取一个容量为8的样本进行分析.
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式即可,不必计算出结果).
(Ⅱ)随机抽出8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95.
若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理分数对应如下表:
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性?如果具有线性相关性,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关性,请说明理由.
参考公式:相关系数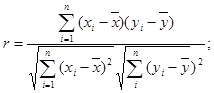
回归直线的方程是: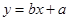 ,
,
其中对应的回归估计值.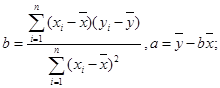
参考数据: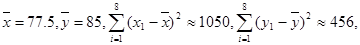
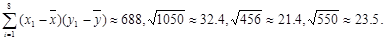
(Ⅰ)如果按性别比例分层抽样,可以得到多少个不同的样本?(只要求写出算式即可,不必计算出结果).
(Ⅱ)随机抽出8位,他们的数学分数从小到大排序是:60、65、70、75、80、85、90、95,物理分数从小到大排序是:72、77、80、84、88、90、93、95.
若规定85分以上(包括85分)为优秀,求这8位同学中恰有3位同学的数学和物理分数均为优秀的概率;
(2)若这8位同学的数学、物理分数对应如下表:
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式:相关系数
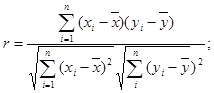
回归直线的方程是:
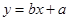 ,
,其中对应的回归估计值.
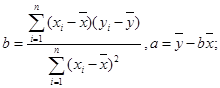
参考数据:
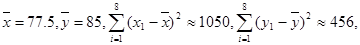
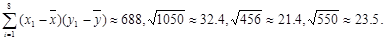
(I)应选女生25×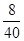 =5(个),男生15×
=5(个),男生15×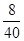 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是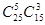 .
.
(II)(1) ;(2)y与x的回归方程是
;(2)y与x的回归方程是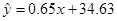 .
.
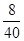 =5(个),男生15×
=5(个),男生15×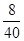 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是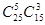 .
.(II)(1)
 ;(2)y与x的回归方程是
;(2)y与x的回归方程是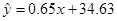 .
.本题考查线性回归分析的初步应用,考查分层抽样,考查条件概率,考查相互独立事件同时发生的概率,考查利用数学知识解决实际问题的能力,是一个比较好的综合题目.
(1)从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析,做出女生和男生在总人数中所占的比例,用比例乘以要抽取的样本容量,得到结果.
(2)①这是一个条件概率,在良好的条件下,两科均为优秀,根据等可能事件的概率和相互独立事件同时发生的概率做出一个学生两科都良好的概率,和两科都优秀的概率,利用条件概率公式得到结果.
②首先求出两个变量的平均数,再利用最小二乘法做出线性回归方程的系数,把做出的系数和x,y的平均数代入公式,求出a的值,写出线性回归方程,得到结果.
解:(I)应选女生25×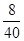 =5(个),男生15×
=5(个),男生15×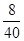 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是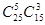 .
.
(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是 ,然后剩下的5个数学分数和物理分数任意对应,种数是
,然后剩下的5个数学分数和物理分数任意对应,种数是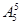 。根据乘法原理满足条件的种数是
。根据乘法原理满足条件的种数是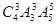
这8位同学的物理分数和数学分数分别对应的种数共有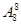 .
.
故所求的概率
(2)变量y与x的相关系数是r=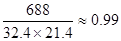 .可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,物理成绩y为纵坐标做散点图
.可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,物理成绩y为纵坐标做散点图
从散点图可以看出这些点大至分布在一条直线附近,并且在逐步上升,
故物理与数学成绩是高度正相关.
设y与x线性回归方程y=bx+a、
根据所给的数据,可以计算出
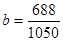 =0.65,a=85-0.65×77.5=34.63,
=0.65,a=85-0.65×77.5=34.63,
所以y与x的回归方程是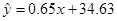 .
.
(1)从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析,做出女生和男生在总人数中所占的比例,用比例乘以要抽取的样本容量,得到结果.
(2)①这是一个条件概率,在良好的条件下,两科均为优秀,根据等可能事件的概率和相互独立事件同时发生的概率做出一个学生两科都良好的概率,和两科都优秀的概率,利用条件概率公式得到结果.
②首先求出两个变量的平均数,再利用最小二乘法做出线性回归方程的系数,把做出的系数和x,y的平均数代入公式,求出a的值,写出线性回归方程,得到结果.
解:(I)应选女生25×
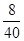 =5(个),男生15×
=5(个),男生15×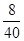 =3(个),可以得到不同的样本个数是
=3(个),可以得到不同的样本个数是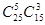 .
.(II)(1)这8位同学中恰有3位同学的数学和物理分数均为优秀,则需要先从物理的4个优秀分数中选出3个与数学优秀分数对应,种数是
 ,然后剩下的5个数学分数和物理分数任意对应,种数是
,然后剩下的5个数学分数和物理分数任意对应,种数是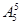 。根据乘法原理满足条件的种数是
。根据乘法原理满足条件的种数是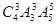
这8位同学的物理分数和数学分数分别对应的种数共有
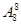 .
.故所求的概率

(2)变量y与x的相关系数是r=
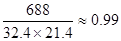 .可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,物理成绩y为纵坐标做散点图
.可以看出,物理与数学成绩是高度正相关.若以数学成绩x为横坐标,物理成绩y为纵坐标做散点图从散点图可以看出这些点大至分布在一条直线附近,并且在逐步上升,
故物理与数学成绩是高度正相关.
设y与x线性回归方程y=bx+a、
根据所给的数据,可以计算出
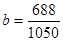 =0.65,a=85-0.65×77.5=34.63,
=0.65,a=85-0.65×77.5=34.63,所以y与x的回归方程是
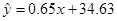 .
.
练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
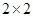 列联表进行独立性检验,经计算
列联表进行独立性检验,经计算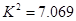 ,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
,则所得到的统计学结论是:有( )的把握认为“学生性别与支持该活动有关系”。
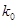
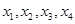 的方差为
的方差为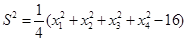 ,则数据
,则数据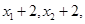
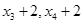 的平均数为( )
的平均数为( ) 越大,相关程度越大
越大,相关程度越大 ,
, 且
且 ,相关程度越大;
,相关程度越大; ,相关程度越小
,相关程度越小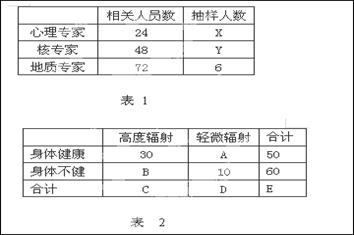
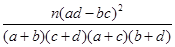
 ,则该单位员工总数为________人.
,则该单位员工总数为________人. )用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是____________,气温波动较大的城市是____________.
)用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是____________,气温波动较大的城市是____________.