题目内容
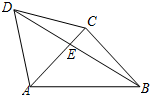 如图,△ACD是等边三角形,△ABC是等腰直角三角形∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形∠ACB=90°,BD交AC于E,AB=2.(Ⅰ)求cos∠CBE的值;(Ⅱ)求AE.
分析:(Ⅰ) 根据△BCD为等腰三角形,∠BCD=∠ACB+∠ACD=90°+60°=150°,可得∠CBE=15°,故cos∠CBE=
cos15°=cos(45°-30°),运算求得结果.
(Ⅱ)由(Ⅰ)知∠ABE=45°-15°=30°,故∠BEC=75°,可得∠AEB=105°,△ABE中,由正弦定理求出
AE的值.
cos15°=cos(45°-30°),运算求得结果.
(Ⅱ)由(Ⅰ)知∠ABE=45°-15°=30°,故∠BEC=75°,可得∠AEB=105°,△ABE中,由正弦定理求出
AE的值.
解答:解:(Ⅰ) 由题意可得等边三角形ACD的边长为
,∵∠BCD=∠ACB+∠ACD=90°+60°=150°.
又△BCD为等腰三角形,∴∠CBE=15°,
∴cos∠CBE=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=
.
(Ⅱ)由(Ⅰ)知∠ABE=45°-15°=30°,故∠BEC=75°.
∴∠AEB=105°,△ABE中,由正弦定理可得
=
,
且sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
,
∴
=
,∴AE=(
-
).
| 2 |
又△BCD为等腰三角形,∴∠CBE=15°,
∴cos∠CBE=cos15°=cos(45°-30°)=cos45°cos30°+sin45°sin30°=
| ||||
| 4 |
(Ⅱ)由(Ⅰ)知∠ABE=45°-15°=30°,故∠BEC=75°.
∴∠AEB=105°,△ABE中,由正弦定理可得
| AE |
| sin30° |
| AB |
| sin105° |
且sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
| ||||
| 4 |
∴
| AE | ||
|
| 2 | ||||||
|
| 6 |
| 2 |
点评:本题考查三角形内角和公式、半角公式、正弦定理的应用,求出∠CBE=15°,∠AEB=105°,是解题的关键,属于
中档题.
中档题.

练习册系列答案
相关题目
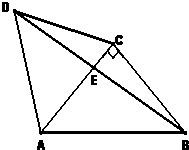 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.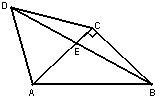 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2,则AE=
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2,则AE= 如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.
如图,△ACD是等边三角形,△ABC是等腰直角三角形,∠ACB=90°,BD交AC于E,AB=2.