题目内容
已知集合A={x||x-2|＜3，x∈R}，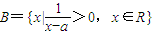
，且A∩B=A，那么实数a的取值范围是 ．
【答案】分析：先由绝对值不等式的解法求出集合A，分式不等式解法求出B．条件A∩B=A等价与A⊆B，将集合的关系转化为元素的关系．
解答：解：A={x|-3＜x-2＜3，}={x|＜-1＜x＜5}，B={x|x＞a}．∵A∩B=A∴A⊆B，∴a≤-1
故答案为：（-∞，-1]
点评：本题考查集合的基本关系，不等式的解法，数形结合的思想进行集合的运算．
解答：解：A={x|-3＜x-2＜3，}={x|＜-1＜x＜5}，B={x|x＞a}．∵A∩B=A∴A⊆B，∴a≤-1
故答案为：（-∞，-1]
点评：本题考查集合的基本关系，不等式的解法，数形结合的思想进行集合的运算．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目