题目内容
由方程x|x|+y|y|=1确定的函数y=f（x）在R上是 （ ）
分析：先利用分类讨论的方法对x，y的取值进行讨论，化去绝对值符号，化简曲线的方程，再结合方程画出图形，由图观察即得．
解答：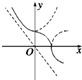
解：①当x≥0且y≥0时，x2+y2=1，
②当x＞0且y＜0时，x2-y2=1，
③当x＜0且y＞0时，y2-x2=1，
④当x＜0且y＜0时，无意义．
由以上讨论作图如右，易知是减函数．
故选D．
解：①当x≥0且y≥0时，x2+y2=1，②当x＞0且y＜0时，x2-y2=1，
③当x＜0且y＞0时，y2-x2=1，
④当x＜0且y＜0时，无意义．
由以上讨论作图如右，易知是减函数．
故选D．
点评：本小题主要考查函数单调性的应用、函数单调性的判断与证明等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想及分类讨论的思想．属于基础题．
练习册系列答案
相关题目