题目内容
设函数y=f（x）由方程x|x|+y|y|=1确定，下列结论正确的是（1）f（x）是R上的单调递减函数；
（2）对于任意x∈R，f（x）+x＞0恒成立；
（3）对于任意a∈R，关于x的方程f（x）=a都有解；
（4）f（x）存在反函数f-1（x），且对于任意x∈R，总有f（x）=f-1（x）成立．
分析：先去掉绝对值，将方程转化为分段函数，再作出分段函数的图象，用数形结合法易得结论．
解答：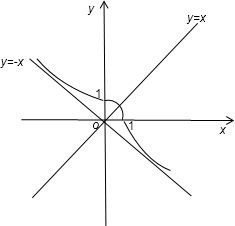
解：去掉绝对值得：f(x)=
作出其图象为：如图所示：
（1）在定义域上为递减函数．正确．
（2）由双曲线的渐近线可知：f（x）的图象在y=-x的上方．正确．
（3）由f（x）的图象向上向下无限延展，f（x）的图象在y=a一定有交点，正确．
（4）由f（x）的图象关于y=x对称，正确．
故答案为：（1）（2）（3）（4）
解：去掉绝对值得：f(x)=
|
作出其图象为：如图所示：
（1）在定义域上为递减函数．正确．
（2）由双曲线的渐近线可知：f（x）的图象在y=-x的上方．正确．
（3）由f（x）的图象向上向下无限延展，f（x）的图象在y=a一定有交点，正确．
（4）由f（x）的图象关于y=x对称，正确．
故答案为：（1）（2）（3）（4）
点评：本题主要考查将方程问题转化为分段函数，进而来研究分段函数的图象和性质，这类问题往往与圆锥曲线有关，综合性较强．
练习册系列答案
阅读快车系列答案
相关题目