题目内容
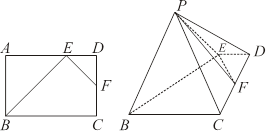
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面 底面
底面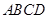 ,且△PAD为等腰直角三角形,
,且△PAD为等腰直角三角形, ,E、F分别为PC、BD的中点.
,E、F分别为PC、BD的中点.
(1)求证:EF//平面PAD;
(2)求证:平面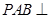 平面
平面 .
.
详见解析
解析试题分析:(1)要证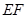 //平面
//平面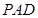 ,可证明
,可证明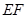 与平面
与平面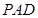 内的一条直线平行,边结
内的一条直线平行,边结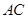 由中位线定理得这条直线就是
由中位线定理得这条直线就是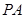 .(2)利用面面垂直的性质可由面面垂直(侧面
.(2)利用面面垂直的性质可由面面垂直(侧面 底面)得线面垂直(
底面)得线面垂直(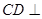 平面
平面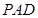 ),进而得到线线垂直(
),进而得到线线垂直(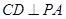 ),再结合线线垂直
),再结合线线垂直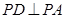 ,又得到线面垂直
,又得到线面垂直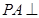 平面
平面 ,证明.平面
,证明.平面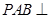 平面
平面 可通过
可通过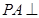 平面
平面 证明.
证明.
试题解析:(1)证明:连接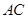 ,
,
因为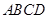 是正方形,
是正方形,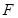 为
为 的中点,所以
的中点,所以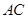 过点
过点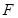 ,且
,且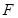 也是
也是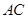 的中点,
的中点,
因为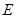 是
是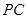 的中点,所以
的中点,所以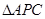 中,
中,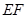 是中位线,所以
是中位线,所以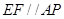
因为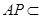 平面
平面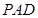 ,
,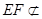 平面
平面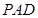 ,所以
,所以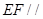 平面
平面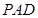
(2)因为侧面 底面
底面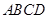 ,
,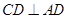
所以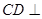 平面
平面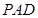
所以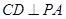
又因为 ,
,
所以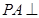 平面
平面 ,
,
因为 平面
平面 ,
,
所以面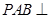 平面
平面

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 AB.直角梯形ACEF中,
AB.直角梯形ACEF中, ,
, 是锐角,且平面ACEF⊥平面ABCD.
是锐角,且平面ACEF⊥平面ABCD.
 ;
;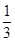 ,试求
,试求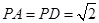 ,
,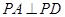 ,底面
,底面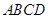 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 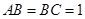 ,O为AD中点.
,O为AD中点.
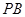 与平面
与平面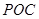 所成角的余弦值;
所成角的余弦值;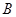 点到平面
点到平面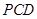 的距离;
的距离;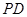 上是否存在一点
上是否存在一点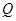 ,使得二面角
,使得二面角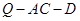 的余弦值为
的余弦值为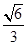 ?若存在,求出
?若存在,求出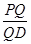 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,点
中,点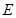 为边
为边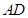 上的点,点
上的点,点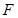 为边
为边 的中点,
的中点, ,现将
,现将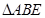 沿
沿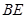 边折至
边折至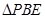 位置,且平面
位置,且平面 平面
平面 .
.
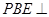 平面
平面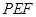 ;
;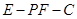 的大小.
的大小. 中,
中,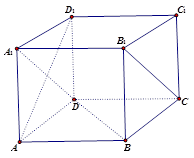
 ;
;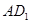 与直线BD所成的角
与直线BD所成的角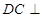 平面
平面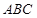 ,
,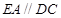 ,
,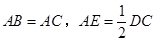 ,
, 为
为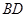 的中点.
的中点.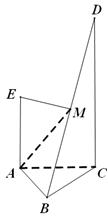
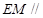 平面
平面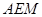
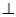 平面
平面 .
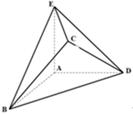
.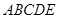 中,
中,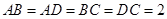 ,
,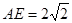 ,
,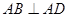 ,且
,且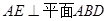 ,
,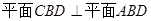 .
.
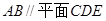 ;
;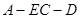 的余弦值.
的余弦值.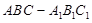 中,
中,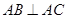 ,
,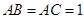 ,
,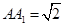 ,D为BC中点.
,D为BC中点.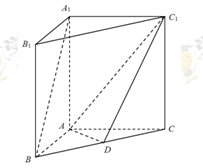
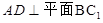 ;
; ;
;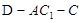 的正弦值.
的正弦值.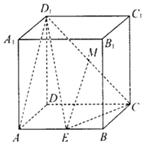
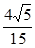 .求线段AE的长.
.求线段AE的长.