题目内容
【题目】选修4-5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若函数![]() 的值域为
的值域为![]() ,且
,且![]() ,求
,求![]() 的取值范围
的取值范围
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)对![]() 分三种情况讨论,分别求解不等式组,然后求并集即可得结果;(2)将函数
分三种情况讨论,分别求解不等式组,然后求并集即可得结果;(2)将函数![]() 化为分段函数,根据分类讨论思想结合分段函数的图象,求出分段函数的值域,根据集合的包含关系列不等式求解即可.
化为分段函数,根据分类讨论思想结合分段函数的图象,求出分段函数的值域,根据集合的包含关系列不等式求解即可.
试题解析:(1)当![]() 时,
时, ![]() .
.
①当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() .
.
②当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() ,此时原不等式无解.
,此时原不等式无解.
③当![]() 时,原不等式可化为
时,原不等式可化为![]() ,解得
,解得![]() .
.
综上可知,原不等式的解集为![]() 或
或![]() .
.
(2)解法:①当![]() 时,
时, 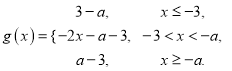
所以函数![]() 的值域
的值域![]() ,
,
因为![]() ,所以
,所以![]() 解得
解得![]() .
.
②当![]() 时,
时, 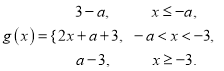
所以函数![]() 的值域
的值域![]() ,
,
因为![]() ,所以
,所以![]() 解得
解得![]() .
.
综上可知, ![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目