题目内容
下列命题中,真命题是( )
分析:A.根据终边相同的角及互补角的正弦值相等,可知A不正确;
B.根据一元二次方程有实数根的充要条件是△≥0,即可判断出是否正确;
C.根据条件及基本不等式即可求出
+
的最小值,进而可判断出是否正确;
D.根据命题“若x=1006且y=1006,则x+y=2012”正确,而此命题的逆否命题是“若x+y≠2012,则x≠1006或y≠1006”,即可判断出是否正确.
B.根据一元二次方程有实数根的充要条件是△≥0,即可判断出是否正确;
C.根据条件及基本不等式即可求出
| 1 |
| a |
| 1 |
| b |
D.根据命题“若x=1006且y=1006,则x+y=2012”正确,而此命题的逆否命题是“若x+y≠2012,则x≠1006或y≠1006”,即可判断出是否正确.
解答:解:A.若sinA=
,则A=kπ+(-1)k
,(k∈Z),故A.不正确;
B.∵△=1-4m≥0,即m≤
时,此方程有实数根,故B不正确;
C.∵a>0,b>0,a+b=1,∴
+
=(a+b)(
+
)=1+1+
+
≥2+2
=4,
即当且仅当a=b=
时取等号,也即
+
的最小值为4,不可能为
,故C不正确;
D.命题“若x=1006且y=1006,则x+y=2012”正确,其逆命题“若x+y=2012,则x=1006,y=1006”不正确;
由此可知此命题的逆否命题正确,而否命题不正确.
故x+y≠2012是x≠0或y≠0的充分不必要条件.即D.正确.
综上可知:真命题是D.
故选D.
| 1 |
| 2 |
| π |
| 6 |
B.∵△=1-4m≥0,即m≤
| 1 |
| 4 |
C.∵a>0,b>0,a+b=1,∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
|
即当且仅当a=b=
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| b |
| 7 |
| 2 |
D.命题“若x=1006且y=1006,则x+y=2012”正确,其逆命题“若x+y=2012,则x=1006,y=1006”不正确;
由此可知此命题的逆否命题正确,而否命题不正确.
故x+y≠2012是x≠0或y≠0的充分不必要条件.即D.正确.
综上可知:真命题是D.
故选D.
点评:充分理解终边相同的角及互补角的正弦值相等、一元二次方程有实数根的充要条件、基本不等式的性质、充要条件的意义是解题的关键.

练习册系列答案
相关题目
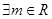 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1