题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-2x,x≥0}\\{-{x}^{2}-2x,x<0}\end{array}\right.$.(Ⅰ)判断f(x)的奇偶性;
(Ⅱ)设函数f(x)在[t,t+4](t∈R)上的最大值为g(t),求g(t)的解析式.
分析 (Ⅰ)根据函数奇偶性的定义即可判断f(x)的奇偶性;
(Ⅱ)分别讨论区间[t,t+4]与函数单调区间的关系,结合一元二次函数单调性的性质进行求解即可.
解答 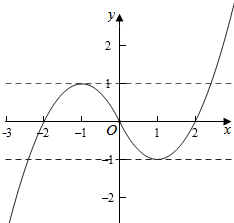 解:(Ⅰ)当x=0时,f(0)=0,
解:(Ⅰ)当x=0时,f(0)=0,
若x<0,则-x>0,
则f(-x)=x2+2x=-(-x2-2x)=-f(x),
若x>0,则-x<0,
则f(-x)=-x2+2x=-(x2-2x)=-f(x),
综上f(-x)=-f(x),即f(x)为奇函数性;
(Ⅱ)作出函数f(x)的图象如图:
由图象知当x=-1时,函数f(x)=1,当x=1时,f(x)=-1,
当x≥0时,由f(x)=x2-2x=1,得x2-2x-1=0,此时x=1+$\sqrt{2}$,此时1+$\sqrt{2}$-(-1)=2+$\sqrt{2}$<4,
当x<0时,由f(x)=-x2-2x=-1,得x2+2x-1=0,此时x=-1-$\sqrt{2}$,此时1-(-1-$\sqrt{2}$)=2+$\sqrt{2}$<4,
而区间[t,t+4]长度为4,区间[t,t+4]的中点为x=t+2,
①若t≤-1,且t+4≥1+$\sqrt{2}$,即$\sqrt{2}-$3≤t≤-1时,此时函数在[t,t+4]上的最大值为g(t)=f(t+4)=(t+4)2-2(t+4)=t2+6t+8,
②若-1≤t+4≤1+$\sqrt{2}$,即-5≤t≤$\sqrt{2}$-3,时,此时函数在[t,t+4]上的最大值为g(t)=f(-1)=1,
③若t+4≤-1,即t≤-5时,此时函数在[t,t+4]上为增函数,此时的最大值为g(t)=f(t+4)=(t+4)2-2(t+4)=t2+6t+8.
点评 本题主要考查函数奇偶性的应用以及函数在闭区间上的最值,利用分类讨论的思想是解决本题的关键.综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | f(x)=sinx | B. | f(x)=sin2x | C. | f(x)=cosx | D. | f(x)=cos2x |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | $-\frac{10}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{10}{3}$或1 | D. | $-\frac{10}{3}$或1 |
| A. | 7∈A | B. | 0∈A | C. | 3∉A | D. | 3.5∉A |
| A. | [6,+∞) | B. | [-∞,2] | C. | [-3,6] | D. | [5,6] |
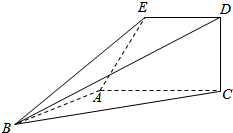 如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=90°,∠EAC=60°,AB=AC. 如图,在直角三角形SOC中,直角边OC的长为4,SC为斜边,OB⊥SC,现将三角形SOC绕SO旋转一周,若△SOC形成的几何体的体积为V,△SOB形成的体积为$\frac{V}{4}$,则V=$\frac{64π}{3}$.
如图,在直角三角形SOC中,直角边OC的长为4,SC为斜边,OB⊥SC,现将三角形SOC绕SO旋转一周,若△SOC形成的几何体的体积为V,△SOB形成的体积为$\frac{V}{4}$,则V=$\frac{64π}{3}$.