题目内容
(本题满分12分)、
某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一日能来回16次,如果每次拖7节车厢,则每日能来回10次,每日来回的次数是车头每次拖挂车厢个数的一次函数,每节车厢能载乘客110人. 问这列火车每天来回多少次,每次应拖挂多少车厢才能使运营人数最多?并求出每天最多运营人数.
【答案】
当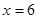 时,
时,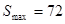 此时y=12,则每日最多运营人数为110×6×12=7920(人)
此时y=12,则每日最多运营人数为110×6×12=7920(人)
【解析】本试题主要是考查了函数在实际生活中的运用。求解函数的最值以及函数的解析式的综合运用。
(1)合理的设出位置变量,设每日来回y次,每次挂x节车厢,由题意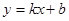
然后运用待定系数法得到解析式
由题意知,每日挂车厢最多时,营运人数最多,设每日营运S节车厢
则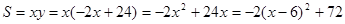 ,运用二次函数的性质得到最值。
,运用二次函数的性质得到最值。
解:设每日来回y次,每次挂x节车厢,由题意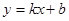
当x=4时y=16 当x=7时y=10得下列方程组:
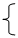 16=4k+b
16=4k+b
10=7k+b 解得:k=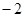 b=24
b=24 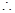
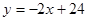
由题意知,每日挂车厢最多时,营运人数最多,设每日营运S节车厢
则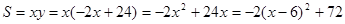
所以当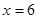 时,
时,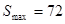 此时y=12
此时y=12
则每日最多运营人数为110×6×12=7920(人)

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面