题目内容
已知两个非零向量a与b,定义|a×b|=|a|·|b|sin θ,其中θ为a与b的夹角.若a=(-3,4),b=(0,2),则|a×b|的值为________.
6
|a|=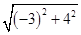 =5,|b|=
=5,|b|= =2,a·b=-3×0+4×2=8,所以cos θ=
=2,a·b=-3×0+4×2=8,所以cos θ=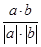 =
=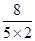 =
= ,又因为θ∈[0,π],所以sin θ=
,又因为θ∈[0,π],所以sin θ=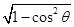 =
=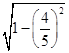 =
=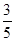 .故根据定义可知|a×b|=|a|·|b|sin θ=5×2×
.故根据定义可知|a×b|=|a|·|b|sin θ=5×2×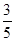 =6.
=6.
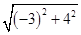 =5,|b|=
=5,|b|= =2,a·b=-3×0+4×2=8,所以cos θ=
=2,a·b=-3×0+4×2=8,所以cos θ=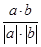 =
=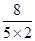 =
= ,又因为θ∈[0,π],所以sin θ=
,又因为θ∈[0,π],所以sin θ=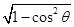 =
=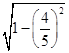 =
=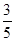 .故根据定义可知|a×b|=|a|·|b|sin θ=5×2×
.故根据定义可知|a×b|=|a|·|b|sin θ=5×2×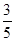 =6.
=6.
练习册系列答案
相关题目



 =a+2b,
=a+2b, =-4a-b,
=-4a-b, =-5a-3b,其中a,b不共线,则四边形ABCD为( )
=-5a-3b,其中a,b不共线,则四边形ABCD为( ) 分别为椭圆
分别为椭圆 的上、下焦点,
的上、下焦点, 是抛物线
是抛物线 的焦点,点
的焦点,点 是
是 与
与 在第二象限的交点, 且
在第二象限的交点, 且
 相切的直线
相切的直线 交椭
交椭 ,若椭圆
,若椭圆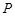 满足
满足 ,求实数
,求实数 的取值范围.
的取值范围.
 的长度与向量
的长度与向量 的长度相等
的长度相等 
 (5)
(5)
 , 且
, 且 , 则
, 则 ( )
( )


