题目内容
(08年崇文区统一练习一)(14分)
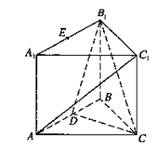
如图,在直三棱柱ABC―A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
(I)求AC1与平面B1BCC1所成角的正切值;
(II)求证:AC1∥平面B1DC;
(III)已知E是A1B1的中点,点P为一动点,记PB1=x. 点P从E出发,沿着三棱柱的棱,按照E→A1→A的路线运动到点A,求这一过程中三棱锥P―BCC1的体积表达式V(x).
|
解:(I)∵直三棱柱ABC―A1B1C1,∴B1B⊥面ABC,
∴B1B⊥AB. 又∵AB⊥BC,∴AB⊥面BCC1B1.…………2分
连结BC1,则∠AC1B为AC1与平面B1BCC1所成角.……3分
依题设知,BC1=2![]() ,在Rt△ABC1中,
,在Rt△ABC1中,
![]() …………5分
…………5分

(II)如图,连结DF,在△ABC1中,∵D、F分别为AB、BC1,
的中点,
∴DF∥AC1,又∵DF![]() 平面B1DC,AC1
平面B1DC,AC1![]() 平面B1DC,
平面B1DC,
∴AC1∥平面B1DC.………………………………10分
(III)PB1=x,![]()
当点P从E点出发到A1点,即![]() 时,由(1)同理可证PB1⊥面BB1C1C,
时,由(1)同理可证PB1⊥面BB1C1C,
![]()
当点P从A1点运动到A点,即![]() 时,
时,![]() .
.
∴三棱锥P―BCC1的体积表达式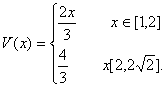 ………………14分
………………14分

练习册系列答案
相关题目