题目内容
数列 1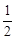 , 2
, 2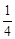 , 3
, 3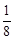 , 4
, 4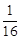 , 5
, 5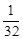 , …, 的前n项之和等于 .
, …, 的前n项之和等于 .
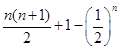
解析考点:数列的求和.
分析:由题意得到数列的通项公式为:an="n+" 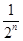 ,然后把和表示为=(1+2+3+…+n)+(
,然后把和表示为=(1+2+3+…+n)+( 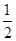 +
+  +
+ 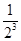 +…+
+…+ 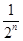 ),分别求和即可.
),分别求和即可.
解:由题意可知数列的通项公式为:an=n+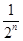
故前n项之和为:(1+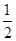 )+(2+
)+(2+ )+(3+
)+(3+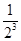 )+…+(n+
)+…+(n+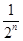 )
)
=(1+2+3+…+n)+(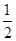 +
+  +
+ 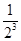 +…+
+…+ 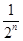 )
)
=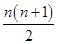 +
+
=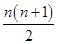 +1-(
+1-(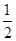 )n
)n
故答案为: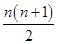 +1-(
+1-(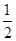 )n
)n

练习册系列答案
相关题目
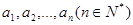 满足条件:
满足条件: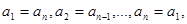
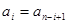 ,
,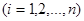 我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列
我们称其为“对称数列”.例如:数列1,2,3,3,2,1 和数列1,2,3,4,3,2,1都为 “对称数列”。已知数列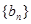 是项数不超过
是项数不超过 的“对称数列”,并使得
的“对称数列”,并使得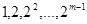 依次为该数列中连续的前
依次为该数列中连续的前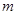 项,则数列
项,则数列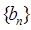 的前2009项和
的前2009项和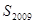 所有可能的取值的序号为
( )
所有可能的取值的序号为
( )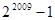 ②
②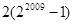 ③
③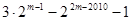 ④
④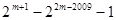
 .
. 的通项
的通项 .
.