题目内容
已知| AB |
| AC |
分析:设平面ABC的单位法向量为
=(x,y,z),根据垂直的两个向量数量积为0,可建立关于x、y、z的两个方程.再结合单位向量模的公式,得到第三个方程,最后联解可得这个单位法向量的坐标.
| a |
解答:解:设平面ABC的单位法向量为
=(x,y,z)
∵
⊥
,∴
•
=2x+2y+z=0…①
同理,
•
=4x+5y+3z=0…②
因为
是单位向量,所以
=
=1…③
联解①②③,得x=
,y=-
,z=
或x=-
,y=
,z=-
∴
=(
,-
,
)或
=(-
,
,-
)
故答案为:(
,-
,
)或(-
,
,-
)
| a |
∵
| a |
| AB |
| a |
| AB |
同理,
| a |
| AC |
因为
| a |
| |a| |
| x2+y2+z2 |
联解①②③,得x=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴
| a |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故答案为:(
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题给出平面内两个已知向量的坐标,要我们求该平面的单位法向量坐标,着重考查了空间两个向量垂直的坐标运算和向量模的公式等知识,属于基础题.

练习册系列答案
相关题目
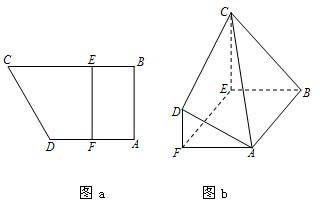
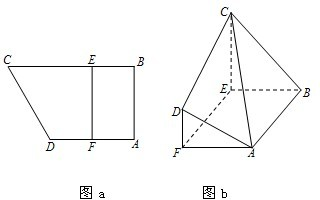 如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.
如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.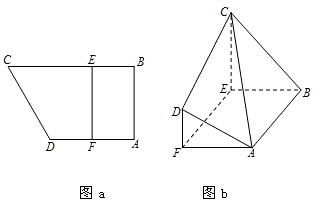 如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.
如图a所示,在直角梯形ABCD中,AB⊥AD,AD∥BC,F为AD的中点,E在BC上,且EF∥AB.已知AB=AD=CE=2,沿线段EF把四边形CDEF折起如图b所示,使平面CDEF⊥平面ABEF.