题目内容
在一次数学竞赛中,共出甲、乙、丙三题,在所有25个参加的学生中,每个学生至少解出一题;在所有没有解出甲题的学生中,解出乙题的人数是解出丙题的人数的2倍;只解出甲题的学生比余下的学生中解出甲题的学生的人数多1;只解出1题的学生中,有一半没有解出甲题.问共有多少学生只解出乙题?分析:设解出甲、乙、丙三题的学生的集合分别是A,B,C,并用三个圆表示之,则重叠部分表示同时解出两题或三题的学生的集合其人数分别以a,b,c,d,e,f,g表示
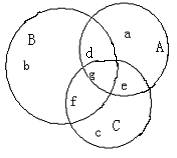
解析:由于每个学生至少解出一题,故
a+b+c+d+e+f+g=25 ①
由于没有解出甲题的学生中,解出乙题的人数是解出
丙题的人数的2倍,故b+f=2(c+f ) ②
由于只解出甲题的学生比余下的学生中解出甲题的学
生的人数多1,故a=d+e+f+1 ③
由于只解出1题的学生中,有一半没有解出甲题,
故a=b+c ④
由②得:b=2c+f, f=2c![]() b ⑤
b ⑤
以⑤代入①消去f得:a+2b![]() c+d+e+f=25 ⑥
c+d+e+f=25 ⑥
以③、④代入⑥得:2b![]() c+2d+2e+2g=24 ⑦ 3b+d+e+g=25 ⑧
c+2d+2e+2g=24 ⑦ 3b+d+e+g=25 ⑧
以2⑧![]() ⑦得: 4b+c=26 ⑨
⑦得: 4b+c=26 ⑨
∵c≥0,∴4b≤26,b≤6![]() .
.
利用⑤、⑨消去c,得f=b![]() 2(26
2(26![]() 4b)=9b
4b)=9b![]() 52 ,
52 ,
∵f≥0,∴9b≥52, b≥![]() .∵
.∵![]() ,∴b=6.
,∴b=6.
即解出乙题的学生有6人.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目