题目内容
已知直线l:x-ny=0(n∈N*),圆M:(x+1)2+(y+1)2=1,抛物线φ:y=(x-1)2,又l与M交于点A、B,l与φ交于点C、D,求| lim |
| n→∞ |
| |AB|2 |
| |CD|2 |
分析:要求
的值,必须先求它与n的关系,,由圆心到直线l的距离和圆的知识可知|AB|2=
.设点C(x1,y1),D(x2,y2),由
整理得nx2-(2n+1)x+n=0,由根与系数的关系可知|CD|2=
(4n+1)(n2+1).由此能够求出
的值.
| lim |
| n→∞ |
| |AB|2 |
| |CD|2 |
| 8n | ||
1+
|
|
| 1 |
| n4 |
| lim |
| n→∞ |
| |AB|2 |
| |CD|2 |
解答:解:设圆心M(-1,-1)到直线l的距离为d,则d2=
.
又r=1,∴|AB|2=4(1-d2)=
.
设点C(x1,y1),D(x2,y2),
由
?nx2-(2n+1)x+n=0,
∴x1+x2=,x1•x2=1.
∵(x1-x2)2=(x1+x2)2-4x1x2=
,(y1-y2)2=(
-
)2=
,
∴|CD|2=(x1-x2)2+(y1-y2)2
=
(4n+1)(n2+1).
∴
=
=
=2.
| (n-1)2 | ||
|
又r=1,∴|AB|2=4(1-d2)=
| 8n | ||
1+
|
设点C(x1,y1),D(x2,y2),
由
|
∴x1+x2=,x1•x2=1.
∵(x1-x2)2=(x1+x2)2-4x1x2=
| 4n+1 | ||
|
| x1 |
| n |
| x2 |
| n |
| 4n+1 |
| n4 |
∴|CD|2=(x1-x2)2+(y1-y2)2
=
| 1 |
| n4 |
∴
| lim |
| n→∞ |
| |AB |2 |
| |CD|2 |
| lim |
| n→∞ |
| 8n5 |
| (4n+1)(n2+1)2 |
| lim |
| n→∞ |
| 8 | ||||
(4+
|
点评:本题属于解析几何与数列极限的综合题.要求极限,需先求
,这就要求掌握求弦长的方法.
| |AB |2 |
| |CD|2 |

练习册系列答案
相关题目

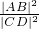 .
.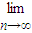
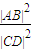 .
.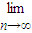
 .
.