题目内容
已知a,b,c,m∈R,且满足a<
<b<
<c,则m的取值范围为
| a-b+mb |
| m |
| b+2c-mc |
| 3-m |
(-∞,0)∪(1,2)
(-∞,0)∪(1,2)
.分析:根据所给不等式,进行等价变形,确定关于m的不等式,即可确定m的取值范围.
解答:解:∵a<
<b<
<c
∴
>0,且
>0,
<0
∵a<b<c
∴b-a>0,b-c<0
∴
>0,
<0,
>0
∴m<0或1<m<2
∴m的取值范围为(-∞,0)∪(1,2)
故答案为:(-∞,0)∪(1,2)
| a-b+mb |
| m |
| b+2c-mc |
| 3-m |
∴
| (b-a)(m-1) |
| m |
| (b-c)(m-2) |
| 3-m |
| b-c |
| 3-m |
∵a<b<c
∴b-a>0,b-c<0
∴
| m-1 |
| m |
| m-2 |
| 3-m |
| 1 |
| 3-m |
∴m<0或1<m<2
∴m的取值范围为(-∞,0)∪(1,2)
故答案为:(-∞,0)∪(1,2)
点评:本题考查参数范围的确定,解题的关键是确定关于m的不等式,属于中档题.

练习册系列答案
相关题目
 ,当m取怎样的值时,长分别为a、b、c、的三线段能构成三角形呢?
,当m取怎样的值时,长分别为a、b、c、的三线段能构成三角形呢? ,当m取怎样的值时,长分别为a、b、c、的三线段能构成三角形呢?
,当m取怎样的值时,长分别为a、b、c、的三线段能构成三角形呢?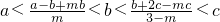 ,则m的取值范围为________.
,则m的取值范围为________.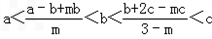 ,则m的取值范围为( ).
,则m的取值范围为( ).