Question

设集合A＝{x｜0<x<1}，B＝{x｜0<x<3}，那么“m∈A”是“m∈B”的

A．充分不必要条件                        B．必要不充分条件

C．充要条件                             D．既不充分也不必要条件

 

Answer 1

【答案】

A

【解析】

试题分析：利用集合的包含关系，判断出集合M与N的关系，利用N是M的真子集，判断两者的关系．因为集合A＝{x｜0<x<1}，B＝{x｜0<x<3}，那么可知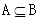,因此可知m∈A”是“m∈B”的充分不必要条件，选A.

考点：充分条件的判定

点评：本题考查利用集合的包含关系判断一个命题是另一个命题的什么条件．当A?B时，A是B的充分不必要条件．