题目内容

双曲线C1：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左准线为l，左焦点和右焦点分别为F1和F2；抛物线C2的准线为l，焦点为F2；C1与C2的一个交点为M，则
|F1F2|
|MF1|
-
|MF1|
|MF2|
等于（　　）
A、-1
B、xOy
C、-
1
2
D、
1
2
分析：先根据题设可知点M同时满足双曲线和抛物线的定义，且在双曲线右支上，进而联立方程可求得|MF1|和|MF2|，代入
|F1F2|
|MF1|
-
|MF1|
|MF2|
答案可得．
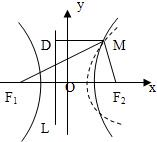解答：精英家教网解：由题设可知点M同时满足双曲线和抛物线的定义，
且在双曲线右支上，故由定义可得
|MF1|-|MF2|=2a
|MF2|=|MD
|MF1|=
c
a
|MD
?|MF1|=
2ac
c-a
，|MF2|=
2a2
c-a

故原式=
2c
2ac
c-a
-
2ac
c-a
2a2
c-a
=
c-a
a
-
c
a
=-1，
故选A．
点评：本题主要考查双曲线和抛物线的定义和性质，几何条件列方程组，消元后化归曲线的基本量的计算，体现数形结合方法的重要性．
练习册系列答案
相关题目
双曲线C1：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左、右焦点分别为F1、F2，抛物线C2：x2=-2py（p＞0）的焦点为F，C1与C2的一个交点为A，知A在x轴上的射影为F1，且A、F、F2三点共线，则双曲线C1的离心率为
 
．
（2012•广西模拟）已知双曲线C1：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的左、右焦点分别为F1、F2，抛物线C2：y2=2px(p＞0)与双曲线C1共焦点，C1与C2在第一象限相交于点P，且|F1F2|=|PF1|，则双曲线的离心率为
2+
3
2+
3
．
（2013•东城区一模）已知F1（-c，0），F2（c，0）分别是双曲线C1：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，双曲线C1和圆C2：x2+y2=c2的一个交点为P，且2∠PF1F2=∠PF2F1，那么双曲线C1的离心率为（　　）
已知点F为双曲线C1：
x2
a2
-
y2
b2
=1（a＞0，b＞0）与抛物线C2：y2=2px（p＞0）的公共焦点，M是C1与C2的一个交点，MF⊥x轴，则双曲线C1的离心率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网