题目内容
13. 如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.
如图,已知AB⊥平面BEC,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形.(Ⅰ)求证:平面ABE⊥平面ADE;
(Ⅱ)求AE与平面CDE所成角的正弦值.
分析 (Ⅰ)取BE的中点F、AE的中点G,连接GD,GD,CF,由已知得CF⊥BF,CF⊥AB,从而DG⊥平面ABE,由此能证明平面ABE⊥平面ADE.
(Ⅱ)补全三棱柱AMN-BEC,取MN中点H,连结AH,EH,说明∠AEH就是AE与平面CDE所成角,然后求解即可.
解答  (Ⅰ)证明:取BE的中点F、AE的中点G,
(Ⅰ)证明:取BE的中点F、AE的中点G,
连接GD,GF,CF,
∵AB⊥平面BCE,△BCE是正三角形,
∴CF⊥BF,CF⊥AB,
∴CF⊥平面ABE,
∵CF∥DG,∴DG⊥平面ABE
∵DG?平面ABE,
∴平面ABE⊥平面ADE.
(Ⅱ) 如图,补全三棱柱AMN-BEC,取MN中点H,连结AH,EH,则△AMN为正三角形,
可得AH⊥MN,
又CD⊥平面AMN,则AH⊥CD,所以,AH⊥平面CDE,
则∠AEH就是AE与平面CDE所成角.
在△AEH中,AH⊥EH,AH=$2\sqrt{3}$,AE=$4\sqrt{2}$,sin∠AEH=$\frac{AH}{AE}$=$\frac{\sqrt{6}}{4}$,
AE与平面CDE所成角的正弦值:$\frac{\sqrt{6}}{4}$.
点评 本题考查平面与平面垂直的证明,直线与平面所成角的求法,是中档题,解题时要注意空间思维能力的培养,注意向量法的合理运用.

练习册系列答案
相关题目
8. 如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )
如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )
 如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )
如图所示,五面体ABCDE中,正△ABC的边长为1,AE⊥平面ABC,CD∥AE,且CD=$\frac{1}{2}$AE.设CE与平面ABE所成的角为α,AE=k(k>0),若α∈[$\frac{π}{6}$,$\frac{π}{4}$],则当k取最大值时,平面BDE与平面ABC所成角的正切值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
2.已知点P($\frac{3}{2}$,-1)在抛物线E:x2=2py(p>0)的准线上,过点P作抛物线的切线,若切点A在第一象限,F是抛物线E的焦点,点M在直线AF上,点N在圆C:(x+2)2+(y+2)2=1上,则|MN|的最小值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{6}{5}$ | C. | 2 | D. | 6$\sqrt{2}$-1 |
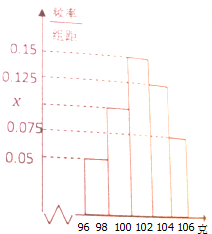 某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106).
某工厂从一批产品中随机抽取40件进行检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106). 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面ABCD为直角梯形,AB∥CD,∠BAD=90°,PA=AD=AB=1,CD=2,E为PC的中点.