Question

设二次函数f(x)满足f(x－2)=f(－x－2)，且图象在y轴上的截距为1，被x轴截得的线段长为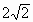，求f(x)的解析式．

Answer 1

答案：
解析：

解法1 设f(x)=＋bx＋c(a≠0)．由f(x－2)=f(－x－2)得4a－b=0①；又，∴②；由已知c=1③．由①、②、③解得b=2，，c=1，∴f(x)= 　　解法2 f(x－2)=f(－x－2)即f(－2＋x)=f(－2－x)，故y=f(x)的图象有对称轴x=－2，可设y=＋k(余略)． 　　解法3 ∵y=f(x)的图象有对称轴x=－2，又，∴y=f(x)与x轴的交点为(，0)，(，0)． 故可设 f(x)=a(．∵f(0)=1，∴a=(余略)．

提示：

三种方法均是用待定系数法求二次函数的解析式，可以看到充分挖掘题目的隐含条件及充分利用图形的直观性，是简化运算的有效手段．