题目内容
y=
(1≤x≤2)反函数是( )
| 2x-x2 |
A、y=1+
| ||
B、y=1+
| ||
C、y=1-
| ||
D、y=1-
|
分析:从条件中函数式y=
(1≤x≤2)中反解出x,再将x,y互换即得到反函数.
| 2x-x2 |
解答:解:在定义域为1≤x≤2,原函数y=
的值域为-1≤y≤1,
∵y=
,
∴y2=2x-x2,
解得x=1±
,
∵1≤x≤2,
∴x=1+
,
∴y=1+
(-1≤x≤1),
故选B.
| 2x-x2 |
∵y=
| 2x-x2 |
∴y2=2x-x2,
解得x=1±
| 1-y2 |
∵1≤x≤2,
∴x=1+
| 1-y2 |
∴y=1+
| 1-x2 |
故选B.
点评:本题主要考查反函数的知识点,首先由已知解析式y=f(x)反求出x=Ф(y),然后交换x、y的位置,最后求出原函数的值域,也就是反函数的定义域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
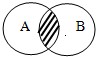 1、设A、B为非空集合,定义集合A*B为如图非阴影部分表示的集合,若A={x|y=
1、设A、B为非空集合,定义集合A*B为如图非阴影部分表示的集合,若A={x|y=| 2x-x2 |
| A、(0,2) |
| B、[0,1]∪[2,+∞) |
| C、(1,2] |
| D、[0,1]∪(2,+∞) |
在某种新型材料的研究中,实验人员获得了下边一组实验数据:
现准备用下列四个函数中的一个近似的表示这些数据的规律,其中最接近的一个是( )
| x | 2.01 | 3.00 | 3.98 | 5.10 | 6.12 |
| y | 1.50 | 4.04 | 7.50 | 12.00 | 17.99 |
| A、y=2x-2 | ||
B、y=
| ||
| C、y=log2x | ||
| D、y=2x |