题目内容
据行业协会预测:某公司以每吨10万元的价格销售某种化工产品,可售出该产品1000吨,若将该产品每吨的价格上涨x%,则销售量将减少mx%,且该化工产品每吨的价格上涨幅度不超过80%,其中m为正常数.(1)当m=
 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?(2)如果涨价能使销售总金额比原销售总金额多,求m的取值范围.
【答案】分析:(1)要求当m= 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大,我们要根据已知条件先构造出函数的解析式,然后根据二次函数求最值的方法,求出销售的总金额的最大值.
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大,我们要根据已知条件先构造出函数的解析式,然后根据二次函数求最值的方法,求出销售的总金额的最大值.
(2)由(1)中的解析式,我们易得=-mx2+100(1-m)x+10000>10000在x∈(0,80]恒成立,然后转化为一个恒成立问题,即可求出m的取值范围.
解答:解:(1)设产品每吨价格上涨x%时,销售总金额为y元.
则y=10(1+x%)′1000(1-mx%)
=-mx2+100(1-m)x+10000
当m= 时,y=-
时,y=- (x-50)2+11250,
(x-50)2+11250,
故当x=50时,ymax=11250(元).
(2)y=-mx2+100(1-m)x+10000x∈(0,80]
y=-mx2+100(1-m)x+10000>10000在x∈(0,80]恒成立
除去x得,-mx+100(1-m)>0在x∈(0,80]恒成立
m为正常数,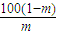 >x,
>x,
而x∈(0,80],
故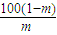 >80,
>80,
∴m∈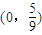 .
.
点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.
 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大,我们要根据已知条件先构造出函数的解析式,然后根据二次函数求最值的方法,求出销售的总金额的最大值.
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大,我们要根据已知条件先构造出函数的解析式,然后根据二次函数求最值的方法,求出销售的总金额的最大值.(2)由(1)中的解析式,我们易得=-mx2+100(1-m)x+10000>10000在x∈(0,80]恒成立,然后转化为一个恒成立问题,即可求出m的取值范围.
解答:解:(1)设产品每吨价格上涨x%时,销售总金额为y元.
则y=10(1+x%)′1000(1-mx%)
=-mx2+100(1-m)x+10000
当m=
 时,y=-
时,y=- (x-50)2+11250,
(x-50)2+11250,故当x=50时,ymax=11250(元).
(2)y=-mx2+100(1-m)x+10000x∈(0,80]
y=-mx2+100(1-m)x+10000>10000在x∈(0,80]恒成立
除去x得,-mx+100(1-m)>0在x∈(0,80]恒成立
m为正常数,
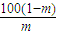 >x,
>x,而x∈(0,80],
故
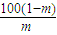 >80,
>80,∴m∈
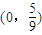 .
.点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大? 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?