题目内容
下列命题:
①若区间D内任意实数x都有f(x+1)>f(x),则y=f(x)在D上是增函数;
②y=-
在定义域内是增函数;
③函数f(x)=
图象关于原点对称;
④既是奇函数又是偶函数的函数一定是f(x)=0 (x∈R);
其中正确的序号是
①若区间D内任意实数x都有f(x+1)>f(x),则y=f(x)在D上是增函数;
②y=-
| 1 |
| x |
③函数f(x)=
| ||
| |x+1|-1 |
④既是奇函数又是偶函数的函数一定是f(x)=0 (x∈R);
其中正确的序号是
③
③
.分析:根据增函数的定义判断①不正确;再由单调区间不能并在一起判断②不对;对于③需要由解析式求出定义域,再判断f(x)与f(-x)的关系,判断函数是奇函数,得到③正确;对于④可以改变定义域得到一个函数进行说明④不对.
解答:解:①、因为x+1与x不能代表定义域内任意的两个自变量,所以根据增函数的定义知,不能确定y=f(x)在D上是增函数,故①不对;
②、y=-
在(-∞,0)和(0,+∞)上是增函数,不能把单调区间并在一起,故②不对;
③、由
解得,-1≤x≤1且x≠0,则函数的定义域是{x|-1≤x≤1且x≠0},
∴f(x)=
=f(x)=
,∴f(-x)=-f(x),则函数f(x)是奇函数,故③正确;
④、如f(x)=0 (x∈[-2,2])既是奇函数又是偶函数,故④不对.
故答案为:③.
②、y=-
| 1 |
| x |
③、由
|
∴f(x)=
| ||
| |x+1|-1 |
| ||
| x |
④、如f(x)=0 (x∈[-2,2])既是奇函数又是偶函数,故④不对.
故答案为:③.
点评:本题是有关函数的单调性与奇偶性的应用,主要利用增(减)函数的定义,奇(偶)函数的定义进行判断,可以结合实际例子进行说明.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
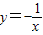 在定义域内是增函数;
在定义域内是增函数;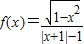 图象关于原点对称;
图象关于原点对称; 在定义域内是增函数;③函数
在定义域内是增函数;③函数 图象关于原点对称;④既是奇函数又是偶函数的函数一定是
图象关于原点对称;④既是奇函数又是偶函数的函数一定是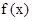 =0
=0  ; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:(
)
; ⑤函数y=f(x+2)图象与函数y=f(2-x)图象关于直线x=2对称;其中正确命题的个数为:(
)