题目内容
设集合M={x|x2+2x=0,x∈R},N={x|x2﹣2x=0,x∈R},则M∪N=( )
| A.{0} | B.{0,2} | C.{﹣2,0} | D.{﹣2,0,2} |
D
分析可得,
M为方程x2+2x=0的解集,则M={x|x2+2x=0}={0,﹣2},
N为方程x2﹣2x=0的解集,则N={x|x2﹣2x=0}={0,2},
故集合M∪N={0,﹣2,2},
故选D.
M为方程x2+2x=0的解集,则M={x|x2+2x=0}={0,﹣2},
N为方程x2﹣2x=0的解集,则N={x|x2﹣2x=0}={0,2},
故集合M∪N={0,﹣2,2},
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
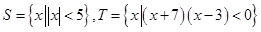 ,则
,则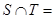 ()
()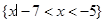
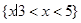
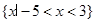
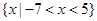
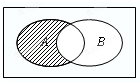
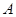 与
与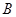 的运算“*”为:
的运算“*”为: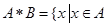 或
或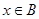 ,但
,但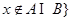 ,按此定义,
,按此定义, ( )
( )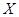
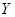
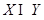
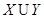
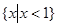 ,Q=
,Q=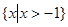 ,则( )
,则( )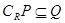
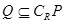
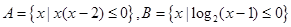 ,则
,则 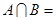 ( )
( )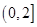
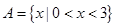 ,
,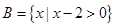 ,则集合
,则集合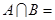 ( )
( )