题目内容
6.已知点A(2,0),B(0,4),点P是过点M(0,-1)的直线l上任意一点,∠APB是锐角,求l的斜率的取值范围.分析 如图所示,以AB为直径画圆Q(1,2),半径R=$\frac{1}{2}|AB|$.由于点P是过点M(0,-1)的直线l上任意一点,∠APB是锐角,可得直线l与⊙Q相离,设直线l:y=kx-1,则圆心Q到直线l的距离d>R,解出即可.
解答 解:如图所示,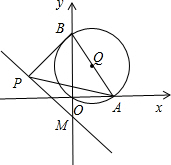
以AB为直径画圆Q(1,2),半径R=$\frac{1}{2}|AB|$=$\frac{1}{2}\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{5}$.
∵点P是过点M(0,-1)的直线l上任意一点,∠APB是锐角,
∴直线l与⊙Q相离,
设直线l:y=kx-1,
则圆心Q到直线l的距离d=$\frac{|k-2-1|}{\sqrt{1+{k}^{2}}}$>$\sqrt{5}$,
化为2k2+3k-2<0,
解得$-2<k<\frac{1}{2}$.
∴l的斜率的取值范围是$(-2,\frac{1}{2})$.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式,考查了数形结合思想方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.已知Sn表示等差数列{an}的前n项和,且$\frac{a_1}{a_5}=\frac{3}{7}$,那么$\frac{S_5}{{{S_{20}}}}$( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{3}$ |
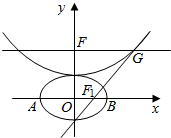 设b>0,椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,抛物线方程为y=$\frac{1}{8}$x2+b,如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的焦点为G,已知抛物线在G点的切线经过椭圆的右焦点F1
设b>0,椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,抛物线方程为y=$\frac{1}{8}$x2+b,如图所示,过点F(0,b+2)作x轴的平行线,与抛物线在第一象限的焦点为G,已知抛物线在G点的切线经过椭圆的右焦点F1