题目内容
若函数 同时满足下列三个性质:①最小正周期为
同时满足下列三个性质:①最小正周期为 ;②图象关于直线
;②图象关于直线 对称;③在区间[
对称;③在区间[ ]上是增函数,则
]上是增函数,则 的解析式可以是 ( )
的解析式可以是 ( )
A. B.
B.
C. D.
D.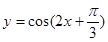
【答案】
A
【解析】略

练习册系列答案
相关题目
题目内容
若函数 同时满足下列三个性质:①最小正周期为
同时满足下列三个性质:①最小正周期为 ;②图象关于直线
;②图象关于直线 对称;③在区间[
对称;③在区间[ ]上是增函数,则
]上是增函数,则 的解析式可以是 ( )
的解析式可以是 ( )
A. B.
B.
C. D.
D.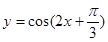
A
【解析】略
