题目内容
已知a是第三象限角,且f(a)=
(1)化简f(a);
(2)若sin(a-
)=
,求f(a)的值.
sin(a-
| ||||
| sin(-a-π)tan(-π-a) |
(1)化简f(a);
(2)若sin(a-
| 3π |
| 2 |
| 1 |
| 5 |
分析:(1)直接根据诱导公式化简即可.
(2)首先根据诱导公式以及已知条件得出sin(a-
)=cosa=
,然后代入即可得出结果.
(2)首先根据诱导公式以及已知条件得出sin(a-
| 3π |
| 2 |
| 1 |
| 5 |
解答:解:(1)f(a)=
=
=-cosa
(2)由(1)知f(a)=-cosa
∵sin(a-
)=cosa=
∴f(a)=-
sin(a-
| ||||
| sin(-a-π)tan(-π-a) |
| -cosa•(-tana)•sina |
| sina•(-tana) |
(2)由(1)知f(a)=-cosa
∵sin(a-
| 3π |
| 2 |
| 1 |
| 5 |
∴f(a)=-
| 1 |
| 5 |
点评:本题考查同角三角函数的基本关系式、诱导公式的应用,考查计算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知a是第三象限角,并且sina=-
,则tana等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
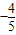 ,则tana等于( )
,则tana等于( )


