题目内容
已知函数 对任意的
对任意的 满足
满足 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A. | B. | C. | D. |
A
解析试题分析:由 即
即 .所以函数
.所以函数 在
在 上递增.所以
上递增.所以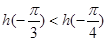 即
即 成立.故选A.
成立.故选A.
考点:1.函数的导数.2.函数的单调性.3.函数的构造的思想.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
已知 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( )
| A.1 | B. | C. | D.3 |
已知偶函数 满足
满足 ,且当
,且当 时,
时, ,则关于
,则关于 的方程
的方程 在
在 上根的个数是( )
上根的个数是( )
A. 个 个 | B. 个 个 | C. 个 个 | D. |
已知函数 对任意的
对任意的 满足
满足 (其中
(其中 是函数
是函数 的导函数),则下列不等式成立的是( )
的导函数),则下列不等式成立的是( )
A. | B. | C. | D. |
函数 的零点所在区间为( )
的零点所在区间为( )
A.(0, ) ) | B.( , , ) ) | C.( ,1) ,1) | D.(1,2) |
函数 的值域是( )
的值域是( )
| A.(0,+∞) | B.[1,+∞) |
| C.(0,1] | D.(0,1) |
已知函数 ,则函数
,则函数 的单调递减区间为( )
的单调递减区间为( )
A. |
B. |
C. |
D. |
 为
为  的导函数,则
的导函数,则  的图象大致是( )
的图象大致是( )
 的图象大致为( )
的图象大致为( )