题目内容
. 19(本小题满分14分)
 已知椭圆 (a>b>0)与直线
已知椭圆 (a>b>0)与直线
x+y-1 = 0相交于A、B两点,且OA⊥OB
(O为坐标原点).
(I) 求 + 的值;
(II) 若椭圆长轴长的取值范围是[,],
求椭圆离心率e的取值范围.
(Ⅰ) 2 (Ⅱ) [ ,]
解析:
(I) 将x+y-1=0代入椭圆方程整理得:(a2+b2)x2-2a2x+a2(1-b2)=0.(*)
设A(x1, y1)、B(x2, y2),则x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
而y1y2=(1-x1)(1-x2) = ![]() .
.
又∵OA⊥OB,∴x1x2+y1y2=0.∴![]() +
+![]() =0.
=0.
∴a2+b2 = 2a2b2∴ + =2 ①
经验证,此时方程(*)有解,∴+ =2. 8分
(2)将b2 = a2-c2,e = 代入①得:2-e2 = 2a2(1-e2).
∴e2 = =1-,而2a∈[,],
∴![]() ≤ e 2 ≤
≤ e 2 ≤ ![]() .而0 < e < 1,∴≤ e ≤ .
.而0 < e < 1,∴≤ e ≤ .
故e的取值范围为[ ,]. 14分

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案( (本小题满分12分)
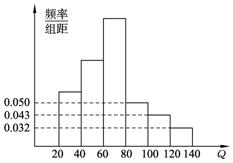
中华人民共和国《道路交通安全法》中将饮酒后违法驾驶机动车的行为分成两个档次:“酒后驾车”和“醉酒驾车”,其检测标准是驾驶人员血液中的酒精含量Q(简称血酒含量,单位是毫克/100毫升),当20≤Q≤80时,为酒后驾车;当Q>80时,为醉酒驾车.济南市公安局交通管理部门于2011年2月的某天晚上8点至11点在市区设点进行一次拦查行动,共依法查出了60名饮酒后违法驾驶机动车者,如图为这60名驾驶员抽血检测后所得结果画出的频率分布直方图(其中Q≥140的人数计入120≤Q<140人数之内).
|
(1) 求此次拦查中醉酒驾车的人数;
(2) 从违法驾车的60人中按酒后驾车和醉酒驾车利用分层抽样抽取8人做样本进行研究,再从抽取的8人中任取3人,求3人中含有醉酒驾车人数x的分布列和期望.
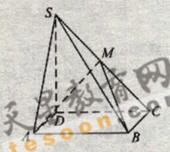
 对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线
对春季某一天气温变化的数据统计显示,气温变化的分布可以用曲线 拟合(
拟合(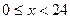 ,单位为小时,
,单位为小时,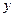 表示气温,单位为摄氏度,
表示气温,单位为摄氏度, ,
,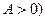 ,现已知这天气温为4至12摄氏度,并得知在凌晨1时整
,现已知这天气温为4至12摄氏度,并得知在凌晨1时整 气温最低,下午13时整气温最高。
气温最低,下午13时整气温最高。