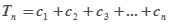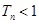题目内容
等差数列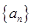 的首项
的首项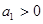 ,前n项和
,前n项和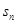 ,当
,当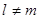 时,
时,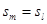 。问n为何值时
。问n为何值时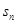 最大?
最大?
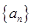 的首项
的首项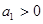 ,前n项和
,前n项和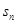 ,当
,当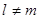 时,
时,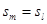 。问n为何值时
。问n为何值时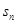 最大?
最大?故若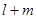 为偶数,当
为偶数,当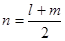 时,
时,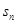 最大。
最大。
当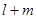 为奇数时,当
为奇数时,当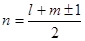 时
时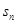 最大
最大
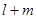 为偶数,当
为偶数,当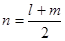 时,
时,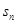 最大。
最大。当
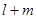 为奇数时,当
为奇数时,当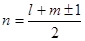 时
时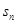 最大
最大【错解分析】等差数列的前n项和是关于n的二次函数,可将问题转化为求解关于n的二次函数的最大值,但易忘记此二次函数的定义域为正整数集这个限制条件。
【正解】由题意知
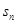 =
=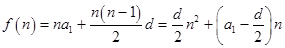 此函数是以n为变量的二次函数,因为
此函数是以n为变量的二次函数,因为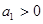 ,当
,当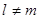 时,
时,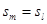 故
故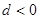 即此二次函数开口向下,故由
即此二次函数开口向下,故由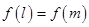 得当
得当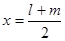 时
时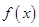 取得最大值,但由于
取得最大值,但由于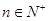 ,故若
,故若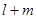 为偶数,当
为偶数,当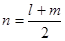 时,
时,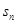 最大。
最大。当
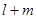 为奇数时,当
为奇数时,当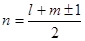 时
时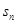 最大。
最大。
练习册系列答案
相关题目
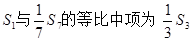 ,且
,且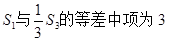
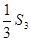 , 求和Tn=a1b1+a2b2+…+anbn
, 求和Tn=a1b1+a2b2+…+anbn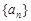 中,已知
中,已知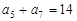 ,则该数列前11项和
,则该数列前11项和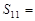
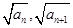 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(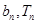 )在直线y=-
)在直线y=-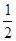 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。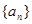 的首项为
的首项为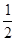 ,
,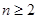 时,
时,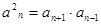 ,数列
,数列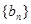 对任意
对任意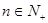 均有
均有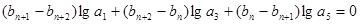
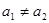 ,求证:数列
,求证:数列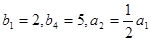 ,数列
,数列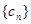 满足
满足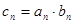 ,记数列
,记数列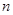 项和为
项和为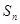 ,求证
,求证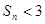 .
.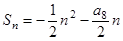 ,则使
,则使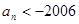 成立的最小正整数
成立的最小正整数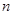 为( )
为( )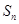 为等差数列{
为等差数列{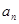 }的前n项和,若
}的前n项和,若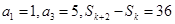 ,则k的值为
,则k的值为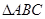 的一个内角为120o,并且三边长构成公差为4的等差数列,则
的一个内角为120o,并且三边长构成公差为4的等差数列,则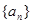 满足条件:
满足条件: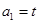 ,
,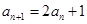
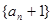 是否为等比数列;
是否为等比数列; 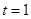 ,令
,令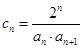 , 记
, 记