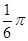题目内容
在棱长为1的正方体内,有两个球相外切并且分别与正方体的面相切.
(1)求这两个球的半径之和;
(2)球的半径是多少时,两球体积之和最小.
答案:
解析:
解析:
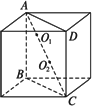
解:(1)如图所示,ABCD为过球心和对棱AB、CD的截面,则AC=![]() .
.
设两个球半径分别为R、r,则AC=AO1+O1O2+O2C=![]() r+(r+R)+
r+(r+R)+![]() R=
R=![]() ,∴R+r=
,∴R+r=![]() .
.

(2)设两个球体积之和为V,则V=![]() π(R3+r3)=
π(R3+r3)=![]() π(R+r)(R2-Rr+r2)=
π(R+r)(R2-Rr+r2)=![]() π(R+r)[(R+r)2-3Rr]=
π(R+r)[(R+r)2-3Rr]=![]() π·
π·![]() ·[3R2-
·[3R2-![]() R+(
R+(![]() )2].
)2].
当R=r=![]() 时,V有最小值.
时,V有最小值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
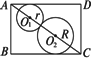
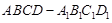 内随机取一点
内随机取一点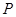 ,则点
,则点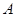 的距离大于1的概率为( )
的距离大于1的概率为( )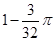 B.
B.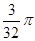 C.
C.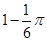 D.
D.