题目内容
设x,y为任意实数,不等式组
表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是
|
[
,
]
| 4 | 2 |
| 3 | 3 |
[
,
]
.| 4 | 2 |
| 3 | 3 |
分析:确定不等式组表示的平面区域,根据指数函数y=ax的图象上存在区域D上的点,即可求得实数a的取值范围.
解答:解:不等式组
表示一个三角形区域,三角形的三个顶点坐标分别为(2,2)(3,3),(4,2)
代入指数函数y=ax可得a的值分别为
、
、
∴实数a的取值范围是[
,
]
故答案为:[
,
]
|
代入指数函数y=ax可得a的值分别为
| 2 |
| 3 | 3 |
| 4 | 2 |
∴实数a的取值范围是[
| 4 | 2 |
| 3 | 3 |
故答案为:[
| 4 | 2 |
| 3 | 3 |
点评:本题考查线性规划,考查指数函数,确定平面区域是关键.

练习册系列答案
相关题目
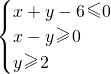 表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是________.
表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是________.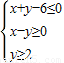 表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是 .
表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是 .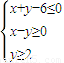 表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是 .
表示区域D,若指数函数y=ax的图象上存在区域D上的点,则实数a的取值范围是 .