题目内容
(1)设全集为R,集合A={t|t=sin(2x-
),
≤x≤
},若不等式t2+at+b≤0的解集是A,求a,b的值.
(2)已知集合M={x|(
)x2-x-6≤1},N={x|log4(x+m)≤1},若M∩N=∅,求实数m的取值范围.
| π |
| 6 |
| π |
| 4 |
| π |
| 2 |
(2)已知集合M={x|(
| 1 |
| 2 |
分析:(1)由x的范围,求出2x-
的范围,根据正弦函数的图象与性质得出此时正弦函数sin(2x-
)的值域,即为t的取值范围,确定出集合A,再由不等式t2+at+b≤0的解集是A,得到集合A中解集中的两个端点为方程x2+ax+b=0的两根,利用韦达定理列出关于a与b的方程,求出方程的解即可得到a与b的值;
(2)把集合M中的不等式右边的“1”变为(
)0,根据
小于1,得到指数函数为减函数,可列出关于x的不等式,求出不等式的解集得到x的范围,确定出集合M,把集合N中的不等式右边的“1”变为
,根据4大于1,得到对数函数为增函数,且根据对数函数的真数大于0,列出关于x的不等式,求出不等式的解集得到x的范围,确定出集合N,然后根据两集合的交集为空集,可得出m的取值范围.
| π |
| 6 |
| π |
| 6 |
(2)把集合M中的不等式右边的“1”变为(
| 1 |
| 2 |
| 1 |
| 2 |
| log | 4 4 |
解答:(本小题满分14分)
解:(1)∵
≤x≤
,∴
≤2x-
≤
,…(2分)
∴sin(2x-
)∈[
,1],
∴A={t|
≤t≤1},…(4分)
∴
,1是方程x2+ax+b=0的两根,…(5分)
∴
,解得:
,…(7分)
(2)由集合M中的不等式(
)x2-x-6≤1=(
)0,
∵
<1,∴指数函数为减函数,
∴x2-x-6≥0,即(x-3)(x+2)≥0,
解得:x≥3或x≤-2,
∴M={x|x≥3或x≤-2},…(9分)
由集合N中的不等式log4(x+m)≤1=
,
∵4>1,∴对数函数为增函数,
∴x+m≤4,且x+m>0,
解得:-m<x≤4-m,
∴N={x|-m<x≤4-m},…(11分)
∵M∩N=∅,
∴
,…(13分)
可得1<m≤2.…(14分)
解:(1)∵
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(2x-
| π |
| 6 |
| 1 |
| 2 |
∴A={t|
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
|
|
(2)由集合M中的不等式(
| 1 |
| 2 |
| 1 |
| 2 |
∵
| 1 |
| 2 |
∴x2-x-6≥0,即(x-3)(x+2)≥0,
解得:x≥3或x≤-2,
∴M={x|x≥3或x≤-2},…(9分)
由集合N中的不等式log4(x+m)≤1=
| log | 4 4 |
∵4>1,∴对数函数为增函数,
∴x+m≤4,且x+m>0,
解得:-m<x≤4-m,
∴N={x|-m<x≤4-m},…(11分)
∵M∩N=∅,
∴
|
可得1<m≤2.…(14分)
点评:此题考查了其他不等式的解法,涉及的知识有:集合中参数的取值问题,指、对数函数的增减性,正弦函数的定义域与值域,韦达定理,以及一元一次不等式的解法,利用了转化的思想,是高考中常考的题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
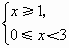 的解集为A,则
的解集为A,则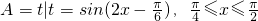 ,若不等式t2+at+b≤0的解集是A,求a,b的值.
,若不等式t2+at+b≤0的解集是A,求a,b的值.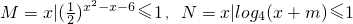 ,若M∩N=Φ,求实数m的取值范围.
,若M∩N=Φ,求实数m的取值范围.